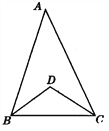
【题目】(1)如图,在△ABC中,∠A=42°,∠ABC和∠ACB的平分线相交于点D,求∠BDC的度数.
(2)在(1)中去掉∠A=42°这个条件,请探究∠BDC和∠A之间的数量关系.
参考答案:
【答案】(1)111° (2)90°+![]() ∠A
∠A
【解析】试题分析:(1)由∠A的度数,根据三角形的内角和定理,求出∠ABC、∠ACB度数,再求出∠DBC与∠DCB的度数和,进而求出∠BDC的度数.
(2)∠BDC+∠DBC+∠DCB=180°,∠A+∠ABC+∠ACB=180°,又有∠ABC+∠ACB=2(∠DBC+∠DCB),可得∠BDC和∠A之间的数量关系.
试题解析:
(1)∵∠ABC+∠ACB =180°-∠A=180°-42°=138°,
又∵BD,CD分别是∠ABC,∠ACB的平分线,
∴∠CBD=![]() ∠ABC,∠BCD=
∠ABC,∠BCD=![]() ∠ACB,
∠ACB,
∴∠CBD+∠BCD=![]() (∠ABC+∠ACB)=69°,
(∠ABC+∠ACB)=69°,
∴∠BDC =180°-(∠CBD+∠BCD)=180°-69°=111°.
(2)90°+![]() ∠A.理由如下:
∠A.理由如下:
∵∠ABC+∠ACB =180°-∠A,
又∵BD,CD分别是∠ABC,∠ACB的平分线,
∴∠CBD=![]() ∠ABC,∠BCD=
∠ABC,∠BCD=![]() ∠ACB,
∠ACB,
∴∠CBD+∠BCD=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A,
∠A,
∴∠BDC =180°-(90°-![]() ∠A)=180°-90°+
∠A)=180°-90°+![]() ∠A=90°+
∠A=90°+![]() ∠A.
∠A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AD是高,AE是角平分线.
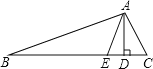
(1)若∠B=20°,∠C=60°,求∠EAD度数;
(2)若∠B=α,∠C=β(β>a),求∠EAD.(用α、β的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】骰子是一种特别的数字立方体(见右图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )
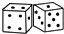
A.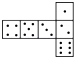
B.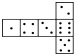
C.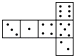
D.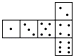
-
科目: 来源: 题型:
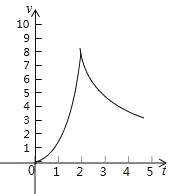
查看答案和解析>>【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.
(3)求弹珠离开轨道时的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级二班45名同学在学校举行的“爱心涌动校园”募捐活动中捐款情况如下表:
捐款数(元)
10
20
30
40
50
捐款人数(人)
8
17
16
2
2
则全班捐款的45个数据众数和中位数是( )
A. 20元,30元B. 50元,30元C. 50元,20元D. 20元,20元
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的两条边长分别为2和5,则它的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若–5xa+5y3+8x3yb=3x3y3,则ab的值是________.
相关试题

