【题目】【问题提出】
用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
【问题探究】
不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以先从特殊入手,通过试验、观察、类比、最后归纳、猜测得出结论.
【探究一】
(1)用3根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
此时,显然能搭成一种等腰三角形.
所以,当n=3时,m=1.
(2)用4根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形.
所以,当n=4时,m=0.
(3)用5根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形.
若分成2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形.
所以,当n=5时,m=1.
(4)用6根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形.
若分成2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形.
所以,当n=6时,m=1.
综上所述,可得:表①

【探究二】
(1)用7根相同的木棒搭一个三角形,能搭成多少种不同的三角形?
(仿照上述探究方法,写出解答过程,并将结果填在表②中)
(2)用8根、9根、10根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
表②

你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…
【问题解决】:
用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(设n分别等于4k﹣1,4k,4k+1,4k+2,其中k是正整数,把结果填在表③中)
表③

【问题应用】:
用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(写出解答过程),其中面积最大的等腰三角形每腰用了 根木棒.(只填结果)
参考答案:
【答案】【探究二】:2;1;2;2;【问题解决】:k;k﹣1;k;k;【问题应用】:672.
【解析】
试题分析:探究二:仿照探究一的方法进行分析即可;
问题解决:根据探究一、二的结果总结规律填表即可;
问题应用:根据规律进行计算求出m的值.
试题解析:(1)用7根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
此时,能搭成二种等腰三角形,即分成2根木棒、2根木棒和3根木棒,则能搭成一种等腰三角形
分成3根木棒、3根木棒和1根木棒,则能搭成一种等腰三角形
当n=7时,m=2.
(2)用8根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
分成2根木棒、2根木棒和4根木棒,则不能搭成一种等腰三角形,分成3根木棒、3根木棒和2根木棒,则能搭成一种等腰三角形,所以,当n=8时,m=1.
用9根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
分成3根木棒、3根木棒和3根木棒,则能搭成一种等腰三角形
分成4根木棒、4根木棒和1根木棒,则能搭成一种等腰三角形
所以,当n=9时,m=2.
用10根相同的木棒搭一个三角形,能搭成多少种不同的等腰三角形?
分成3根木棒、3根木棒和4根木棒,则能搭成一种等腰三角形
分成4根木棒、4根木棒和2根木棒,则能搭成一种等腰三角形
所以,当n=10时,m=2.
故答案为:2;1;2;2.
问题解决:由规律可知,答案为:k;k﹣1;k;k.
问题应用:2016÷4=504,504﹣1=503,当三角形是等边三角形时,面积最大,2016÷3=672,∴用2016根相同的木棒搭一个三角形,能搭成503种不同的等腰三角形,其中面积最大的等腰三角形每腰用672根木棒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】制造某种产品成本100元,计划经过两年成本降低为64元,则平均每年降低( )
A.18%B.20%C.36%D.以上答案均错
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或方程组解应用题:
为了响应市政府“绿色出行”的号召,小张上下班由自驾车方式改为骑自行车方式.已知小张单位与他家相距20千米,上下班高峰时段,自驾车的平均速度是自行平均车速度的2倍,骑自行车所用时间比自驾车所用时间多
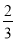 小时.求自驾车平均速度和自行车平均速度各是多少?
小时.求自驾车平均速度和自行车平均速度各是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】通讯卫星的高度是3.6×107米,电磁波在空中的传播速度是3×108米/秒,从地面发射的电磁波被通讯卫星接受并同时反射给地面需要( )
A.3.6×10-1秒
B.1.2×10-1秒
C.2.4×10-2秒
D.2.4×10-1秒 -
科目: 来源: 题型:
查看答案和解析>>【题目】“ ”是规定的这样一种新运算,法则是: ab=a2+2ab .例如 3(2)=32+2×3×(2)=12 .
(1)试求 2(1) 的值;
(2)若 2x=4 ,求 x 的值;
(3)若 (2)x = 2+x ,求 x 的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】画图题:
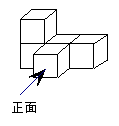

(1)由大小相同的小立方块搭成的几何体如左图,请在右图的方格中画出该几何体的俯视图和左视图。
(2)用小立方体搭一几何体,使得它的俯视图和左视图与你在右图方格中所画的图一致,则这样的几何体最少要个小立方块,最多要个小立方块。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,
交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.

(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
相关试题

