【题目】如图1,直线AB上有一点P,点M、N分别为线段PA、PB的中点,AB=14.
(1)若点P在线段AB上,且AP=8,求线段MN的长度;
(2)若点P在直线AB上运动,设AP=x,BP=y,请分别计算下面情况时MN的长度:
①当P在AB之间(含A或B);
②当P在A左边;
③当P在B右边;
你发现了什么规律?
(3)如图2,若点C为线段AB的中点,点P在线段AB的延长线上,下列结论:①![]() 的值不变;②
的值不变;②![]() 的值不变,请选择一个正确的结论并求其值.
的值不变,请选择一个正确的结论并求其值.
图1
![]() ,
,
图2
![]() ,
,
参考答案:
【答案】(1)7.(2)①点P在AB之间,MN=![]() (x+y);②点P在A左边,MN=
(x+y);②点P在A左边,MN=![]() (y-x);③点P在BA的延长线上,MN=
(y-x);③点P在BA的延长线上,MN=![]() (x-y);(3)选择②①
(x-y);(3)选择②①![]() =
=![]() (在变化);②
(在变化);②![]() =2
=2
【解析】
(1)由AP=8且点M是AP的中点易得MP=![]() AP=4,BP=AB-AP=6,再由点N是PB的中点可知PN=
AP=4,BP=AB-AP=6,再由点N是PB的中点可知PN=![]() PB=3,则MN=MP+PN=7;
PB=3,则MN=MP+PN=7;
(2)根据线段中点的性质,可得MP和NP的表达式,再根据线段的和差关系分别计算三种情况下MN的长度即可;
(3)根据线段的和差,分别可得PA-PB=AB,PA+PB=PC+AC+PC-BC=2PC,再根据分式的性质即可判断.
解:(1)∵AP=8,点M是AP的中点,
∴MP=![]() AP=4,
AP=4,
∴BP=AB-AP=6.
又∵点N是PB的中点,
∴PN=![]() PB=3,
PB=3,
∴MN=MP+PN=7.
(2)①点P在AB之间,MN=MP+PN=![]() =
=![]() (x+y);
(x+y);
②点P在A左边,MN=PN-MP=![]() -
-![]() =
=![]() (y-x);
(y-x);
③点P在BA的延长线上,MN=MP-PN=![]() -
-![]() ==
==![]() (x-y).
(x-y).
(3)选择②.
①![]() ,由于PC长度不固定,故
,由于PC长度不固定,故![]() 的值是变化的;
的值是变化的;
②![]() ,是定值,
,是定值,
故正确的结论是②,其值为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,D1是△ABC的边AB上的一点,则图中有哪几个三角形?
(2)如图2,D1,D2是△ABC的边AB上的两点,则图中有哪几个三角形?
(3)如图3,D1,D2,…,D10是△ABC的边AB上的10个点,则图中共有多少个三角形?
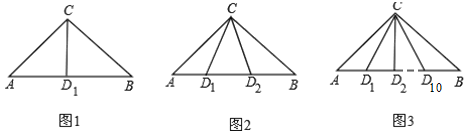
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将点P(2,
 )绕原点O顺时针旋转90°后得到点P′,则点P′的坐标是( )
)绕原点O顺时针旋转90°后得到点P′,则点P′的坐标是( )A. (-2,
 ) B. (
) B. ( ,2) C. (2,-
,2) C. (2,- ) D. (
) D. ( ,-2)
,-2) -
科目: 来源: 题型:
查看答案和解析>>【题目】在篮球比赛中,某队员连续10场比赛中每场的得分情况如下所示:
场次(场)
1
2
3
4
5
6
7
8
9
10
得分(分)
13
4
13
16
6
19
4
4
7
18
则这10场比赛中该队员得分的中位数和众数分别是( )
A.10,4
B.10,13
C.11,4
D.12.5,13 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.为检测某市正在销售的酸奶质量,应采用抽样调查的方式
B.两名同学连续六次的数学测试平均分相同,那么方差较大的同学的数学成绩更稳定
C.抛掷一个正方体骰子,点数为奇数的概率是
D.“打开电视,正在播放动画片”是必然事件 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A(
 ,0),B(0,4),则点B2016的横坐标为( )
,0),B(0,4),则点B2016的横坐标为( )
A.5
B.12
C.10070
D.10080 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在扇形OAB中,∠O=60°,OA=4
 ,四边形OECF是扇形OAB中最大的菱形,其中点E,C,F分别在OA,
,四边形OECF是扇形OAB中最大的菱形,其中点E,C,F分别在OA,  ,OB上,则图中阴影部分的面积为 .
,OB上,则图中阴影部分的面积为 . 
相关试题

