【题目】在平面直角坐标系中,点A(t+1,t+2),点B(t+3,t+1),将点A向右平移3个长度单位,再向下平移4个长度单位得到点C.
(1)用t表示点C的坐标为_______;用t表示点B到y轴的距离为___________;
(2)若t=1时,平移线段AB,使点A、B到坐标轴上的点![]() 、
、![]() 处,指出平移的方向和距离,并求出点
处,指出平移的方向和距离,并求出点![]() 、
、![]() 的坐标;
的坐标;
(3)若t=0时,平移线段AB至MN(点A与点M对应),使点M落在x轴的负半轴上,三角形MNB的面积为4,试求点M、N的坐标.
参考答案:
【答案】 C(t+4,t-2) ![]()
【解析】分析:(1)根据平移规律即可得到结论;
(2)把线段AB分别向左平移2个单位,向下平移2个单位即可得到结论;
(3)当t=0时,得到 A(1,2),B(3,1),设A下平移2个单位,再左平移a个单位到达x轴负半轴,得到M(1-a,0),N(3-a,-1),用割补法表示出MNB的面积,解方程即可.
详解:(1)C(t+4,t-2);![]()
(2)当t=1时,A(2,3),B(4,2)将AB左平移2个单位得![]() (0,3);
(0,3);![]() (2,2);
(2,2);
将AB下平移2个单位得![]() (2,1);
(2,1);![]() (4,0)
(4,0)

(3)若t=0,则A(1,2),B(3,1)设A下平移2个单位,再左平移a个单位到达x轴负半轴,∴M(1-a,0),N(3-a, -1),
∴(3-1+a)![]() 2-
2-![]() (3-1+a)
(3-1+a)![]() 1-
1-![]() (3-a-1+a)
(3-a-1+a)![]() 1-
1-![]() (3-3+a)
(3-3+a)![]() 2=4,
2=4,
∴a=4,∴M(-3,0),N(-1,-1).

-
科目: 来源: 题型:
查看答案和解析>>【题目】.如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点.
(1)试判断AB、AC之间的大小关系,并给出证明;
(2)在上述题设条件下,当△ABC为正三角形时,点E是否AC的中点?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A、C分别在x轴上、y轴上,CB//OA,OA=8,若点B的坐标为(a,b),且b=
 .
.(1)直接写出点A、B、C的坐标;
(2)若动点P从原点O出发沿x轴以每秒2个单位长度的速度向右运动,当直线PC把四边形OABC分成面积相等的两部分停止运动,求P点运动时间;
(3)在(2)的条件下,在y轴上是否存在一点Q,连接PQ,使三角形CPQ的面积与四边形OABC的面积相等?若存在,求点Q的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的有( )
A.π是有理数
B.棱柱的底面是多边形
C.两点之间,直线最短
D.球体可以展开成平面图形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
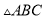 中,已知
中,已知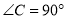 ,
, 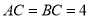 ,
, 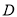 是
是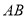 的中点,点
的中点,点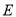 、
、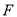 分别在
分别在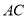 、
、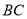 边上运动(点
边上运动(点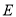 不与点
不与点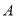 、
、 重合),且保持
重合),且保持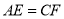 ,连接
,连接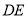 、
、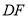 、
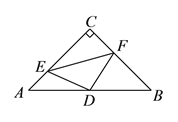
、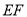 .在此运动变化的过程中,有下列结论,其中正确的结论是( )
.在此运动变化的过程中,有下列结论,其中正确的结论是( )①四边形
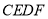 有可能成为正方形;②
有可能成为正方形;②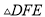 是等腰直角三角形;
是等腰直角三角形;③四边形
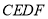 的面积是定值;④点
的面积是定值;④点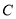 到线段
到线段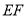 的最大距离为
的最大距离为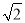 .
.
A. ①④ B. ①②③ C. ①②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形边长都是
 ,图中虚线叫做格线,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形(只要求画出图形,不写作法和结
,图中虚线叫做格线,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形(只要求画出图形,不写作法和结论,作图需用黑笔描画):
(
 )使三角形为直角三角形,且不以格线为任意一边(在图
)使三角形为直角三角形,且不以格线为任意一边(在图 中画一个即可);
中画一个即可);(
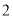 )使三角形的三边长分别为
)使三角形的三边长分别为 ,
,  ,
,  (在图
(在图 中画一个即可);
中画一个即可);(
 )使三角形为钝角三角形且面积为
)使三角形为钝角三角形且面积为 (在图
(在图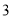 中画一个即可).
中画一个即可).


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,等腰
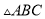 的周长为
的周长为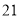 ,底边为
,底边为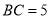 ,
, 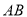 的垂直平分线
的垂直平分线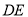 交
交 于点
于点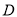 ,交
,交 于点
于点 .
.(
 )求
)求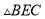 的周长;
的周长;(
 )若
)若 ,
, 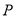 为
为 上一点,连结
上一点,连结 ,
,  ,求
,求 的最小值.
的最小值.
相关试题

