【题目】已知二次函数y=x2﹣4x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2﹣4x+m=0的两个实数根是( )
A.x1=1,x2=﹣1
B.x1=﹣1,x2=2
C.x1=﹣1,x2=0
D.x1=1,x2=3
参考答案:
【答案】D
【解析】解:∵二次函数y=x2﹣4x+m(m为常数)的图象与x轴的一个交点为(1,0), ∴关于x的一元二次方程x2﹣4x+m=0的一个根是x=1.
∴设关于x的一元二次方程x2﹣4x+m=0的另一根是t.
∴1+t=4,
解得 t=3.
即方程的另一根为3.
故选:D.
根据抛物线与x轴交点的性质和根与系数的关系进行解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌LED电视机经过连续两次降价,每台售价由原来的4000元降到了2980元,设平均每次降价的百分率为x,则下列方程中正确的是( )
A.4000(1+x)2=2980
B.2980(1+x)2=4000
C.2980(1﹣x)2=4000
D.4000(1﹣x)2=2980 -
科目: 来源: 题型:
查看答案和解析>>【题目】盒中有4枚黑棋和2枚白棋,这些棋除颜色外无其他差别,在看不到盒中棋子颜色的前提下,从盒中随机摸出3枚棋,下列事件是不可能事件的是( )
A. 摸出的3枚棋中至少有1枚黑棋B. 摸出的3枚棋中有2枚白棋
C. 摸出的3枚棋都是黑棋D. 摸出的3枚棋都是白棋
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=
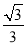 x+m与x轴交于A点,且经过点B(﹣
x+m与x轴交于A点,且经过点B(﹣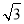 ,2).已知抛物线C:y=ax2+bx+9与x轴只有一个公共点,恰为A点.
,2).已知抛物线C:y=ax2+bx+9与x轴只有一个公共点,恰为A点.(1)求m的值及∠BAO的度数;
(2)求抛物线C的函数表达式;
(3)将抛物线C沿x轴左右平移,记平移后的抛物线为C1,其顶点为P.
平移后,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C1上?
如能,求出此时顶点P的坐标;如不能,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】伟大的文学家、杰出的社会活动家高尔基说:“书籍,是人类进步的阶梯”,阅读使你增长知道,陶冶情操.李楠同学在课外阅读《三国演义》时,她将书翻到某一页,看完后往前翻了10页,然后她又往后翻了8页,这时她发现这三页的页码之和刚好是100,那么该书的这三页的页码分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在高速公路上,从3千米处开始,每隔4千米经过一个限速标志牌,并且从10千米处开始,每隔9千米经过一个速度监控仪,刚好在19千米处第一次同时经过这两种设施,那么,第二次同时经过这两种设施是在( )千米处.
A. 36 B. 37 C. 55 D. 91
-
科目: 来源: 题型:
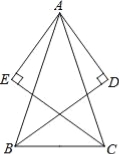
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BD平分∠ABC,CE平分∠ACB,过点A分别作BD、CE的垂线段AD、AE,垂足为D、E,求证:AD=AE.
相关试题

