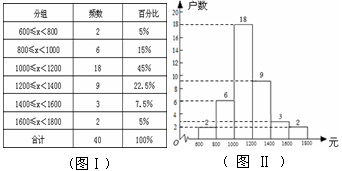
【题目】暑假期间,学校布置了综合实践活动任务,王涛小组四人负责调查本村的500户农民的家庭收入情况,他们随机调查了40户居民家庭的收入情况(收入取整数,单位:元),并制定了频数分布表(如图Ⅰ)和频数分布直方图(如图Ⅱ).


根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该村属于中等收入(不低于1000元小于1600元)的大约有多少户?
参考答案:
【答案】(1)(2)如图所示;(3)375户
【解析】
试题(1)(2)根据各小组的频数之和等于样本总个数,各小组的频率之和等于1求解即可;
(3)先求出该村属于中等收入的居民家庭所占的百分比,再乘以500即可得到结果.
解:(1)(2)如图所示:

(3)(18+9+3)÷40×500=375(户)
答:估计该村属于中等收入(不低于1000元小于1600元)的大约有375户.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.

(1)求抛物线的解析式及点C的坐标;
(2)求证:△ABC是直角三角形;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,则∠AEB的度数为__________.
(2)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是【 】

A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系为:____________________(直接写出结果).
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP,CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系为:____________________(直接写出结果).
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP,CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:如图AB∥CD,∠1=∠2,∠3=∠4,试说明AD∥BE.
解:∵AB∥CD(已知)
∴∠4=∠1+_____(_______)
∵∠3=∠4(已知)
∴∠3=∠1+_____(_______)
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(_______)
即∠_____=∠_____
∴∠3=∠_____(_______)
∴AD∥BE(_______).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( )
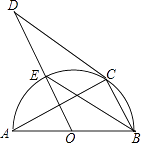
A.AC⊥BC
B.BE平分∠ABC
C.BE∥CD
D.∠D=∠A
相关试题

