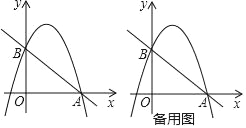
【题目】已知:如图,抛物线y=﹣x2+bx+C经过点B(0,3)和点A(3,0)
(1)求该抛物线的函数表达式和直线AB的函数表达式;
(2)若直线l⊥x轴,在第一象限内与抛物线交于点M,与直线AB交于点N,请在备用图上画出符合题意的图形,并求点M与点N之间的距离的最大值或最小值,以及此时点M,N的坐标.
参考答案:
【答案】(1) 抛物线的函数表达式是y=﹣x2+2x+3;直线AB的函数表达式是y=﹣x+3;(2) 点M与点N之间的距离有最大值![]() ;点M坐标为(
;点M坐标为(![]() ,
,![]() )点N的坐标为(
)点N的坐标为(![]() ,
,![]() ).
).
【解析】整体分析:
(1)把点B(0,3)和点A(3,0)代入到y=-x2+bx+c和一次函数的一般式中求解;(2)设直线l的横坐标为a,分别用a表示出点M,N的坐标,然后用a表示出MN的长,用配方法即可求出MN的最大值.
解:(1)∵抛物线y=-x2+bx+c经过点B(0,3)和点A(3,0),
![]() 解得
解得![]()
抛物线的函数表达式是y=-x2+2x+3;
设直线AB:y=kx+m,根据题意得![]() ,解得
,解得![]() ,
,
直线AB的函数表达式是y=-x+3;
(2)如图,设直线l的横坐标为a,
则点M的坐标为(a,-a2+2a+3),点N的坐标是(a,-a+3),
又点M,N在第一象限,
∴|MN|=-a2+2a+3-(-a+3)=-a2+3a,
又|MN|=-a2+3a=-(a2-3a+![]() )+
)+![]() =
=![]() ,
,
当a=![]() 时,|MN|有最大值,最大值为
时,|MN|有最大值,最大值为![]() ,
,
即点M与点N之间的距离有最大值![]() ,
,
此时点M坐标为(![]() ,
,![]() ),点N的坐标为
),点N的坐标为![]() .
.
-
科目: 来源: 题型:
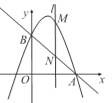
查看答案和解析>>【题目】小明学习电学知识后,用四个开关按键(每个开关键闭合的可能性相等)、一个电源和一个灯泡设计了一个电路图
(1)若小明设计的电路图(四个开关按键都处于打开状态)如图所示,求任意闭合一个开关按键,灯泡能发光的概率;
(2)若小明设计的电路图(四个开关按键都处于打开状态)如图所示,求同时闭合其中的两个开关按键,灯泡能发光的概率.(用列表或树状图法)
-
科目: 来源: 题型:
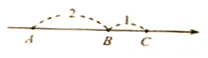
查看答案和解析>>【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示. 设点A,B,C所对应数的和是p.
(1)若以B为原点,则点A,C所对应的数为 、 ,p的值为 ;若以C为原点,p 的值为 ;
(2)若原点O在图中数轴上点C的右边,且CO=28,求p的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个粒子在第一象限内及x轴,y轴上运动,第1分钟从原点运动到
 ,第2分钟从
,第2分钟从 运动到
运动到 ,而后它接着按图中箭头所示的与x轴y轴平行的方向来回运动,且每分钟移动1个长度单位.在第2019分钟时,这个粒子所在位置的坐标是( )
,而后它接着按图中箭头所示的与x轴y轴平行的方向来回运动,且每分钟移动1个长度单位.在第2019分钟时,这个粒子所在位置的坐标是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的弦,半径OA=2,OA和AB的长度是关于x的一元二次方程x2﹣4x+a=0的两个实数根.
(1)求弦AB的长度;
(2)计算S△AOB;
(3)⊙O上一动点P从A点出发,沿逆时针方向运动一周,当S△POA=S△AOB时,求P点所经过的弧长(不考虑点P与点B重合的情形).

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着手机的普及,微信
 一种聊天软件
一种聊天软件 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况 超额记为正,不足记为负
超额记为正,不足记为负 单位:斤
单位:斤 ;
;星期
一
二
三
四
五
六
日
与计划量的差值







(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
-
科目: 来源: 题型:
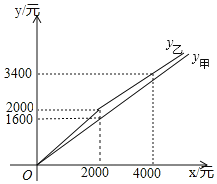
查看答案和解析>>【题目】长沙市的“口味小龙虾”冠绝海内外,如“文和友老长沙龙虾馆”订单排队上千号.某衣贸市场甲、乙两家农贸商店售卖小龙虾,甲、乙平时以同样的价格出售品质相同的小龙虾,“中非贸易博览会”期间,甲、乙两家商店都让利酬宾,付款金额y甲,y乙(单位:元)与原价x(单位:元)之间的函数关系如图所示.
(1)请求出y甲,y乙关于x的函数关系式;
(2)“中非贸易博览会”期间,如果你是龙虾馆采购员,如何选择甲、乙两家商店购买小龙虾更省钱?
相关试题

