【题目】在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF. 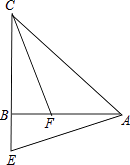
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=60°,求∠ACF的度数.
参考答案:
【答案】
(1)证明:在Rt△ABE和Rt△CBF中,
∵ ![]() ,
,
∴Rt△ABE≌Rt△CBF(HL)
(2)如图,∵在△ABC中,AB=CB,∠ABC=90°,
∴∠ACB=∠CAB=45°,
∴∠BAE=∠CAE﹣∠CAB=15°.
又由(1)知,Rt△ABE≌Rt△CBF,
∴∠BAE=∠BCF=15°,
∴∠ACF=∠ACB﹣∠BCF=30°.即∠ACF的度数是30°
【解析】(1)在Rt△ABE和Rt△CBF中,由于AB=CB,AE=CF,利用HL可证Rt△ABE≌Rt△CBF;(2)由等腰直角三角形的性质易求∠BAE=∠CAE﹣∠CAB=15°.利用(1)中全等三角形的对应角相等得到∠BAE=∠BCF=15°,则∠ACF=∠ACB﹣∠BCF=30°.即∠ACF的度数是30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的命题个数为( )
①所有的等腰三角形都相似;
②有一对锐角相等的两个直角三角形相似;
③所有的正方形都相似;
④四个角对应相等的两个梯形相似.
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果向东运动8m记作+8m,那么向西运动5m应记作 m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,函数y=x2的图象经过点M(x1,y1),N(x2,y2)两点,若﹣2<x1<0,2<x2<4,则y1_____y2.(用“<”、“=”或“>”号连接)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF.

(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解本校七年级学生课外阅读的喜好,随机抽取该校七年级部分学生进行问卷调査(每人只选一种书籍).下图是整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
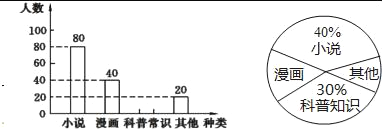
(1)这次活动一共调查了 名学生;
(2)在扇形统计图中,“其他”所在扇形的圆心角等于 度;
(3)补全条形统计图;
(4)若该年级有600名学生,请你估计该年级喜欢“科普常识”的学生人数约是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
甲、乙两人同时从相距25千米的A地去B 地,甲骑车乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40分钟,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
相关试题

