【题目】在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20. 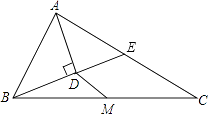
(1)求证:BD=DE;
(2)求DM的长.
参考答案:
【答案】
(1)证明:∵AD平分∠BAC
∴∠BAD=∠DAE
∵AD⊥BD
∴∠ADB=∠ADE=90°
在△ADB与△ADE中

∴△ADB≌△ADE
∴BD=DE
(2)∵△ADB≌△ADE
∴AE=AB=12
∴EC=AC﹣AE=8
∵M是BC的中点,BD=DE
DM= ![]() EC=4
EC=4
【解析】(1)根据条件可证明△ADB≌△ADE,从而可得BD=DE;(2)由(1)可知:EC=AC﹣AB=8,然后根据中位线即可求出DM
【考点精析】本题主要考查了三角形中位线定理的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年4月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了如下两种不完整的统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有 ,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形的圆心角为 度;
(3)学校准备从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE. 求证:
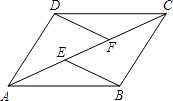
(1)△AFD≌△CEB;
(2)四边形ABCD是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:
 ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于 度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据:
 ≈1.414,
≈1.414, ≈1.732)
≈1.732) -
科目: 来源: 题型:
查看答案和解析>>【题目】点P(3,-2)关于y轴的对称点的坐标是( )
A. (-3,-2) B. (3,2)
C. (-3,2) D. (-3,1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2014年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2016年底三年共累计投资9.5亿元人民币建设廉租房.若在这两年内每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)若这两年内的建设成本不变,求到2016年底共建设了多少万平方米的廉租房?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△OAB中,OA=OB=10,∠AOB=80°,以点O为圆心,6为半径的优弧
 分别交OA、OB于点M、N.
分别交OA、OB于点M、N.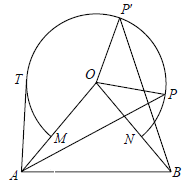
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′. 求证:AP = BP′;
(2)点T在左半弧上,若AT与弧
 相切于点T,求点T到OA的距离;
相切于点T,求点T到OA的距离;(3)设点Q在优弧
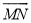 上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
相关试题

