搜索
【题目】如图，E，F是四边形ABCD的对角线AC上两点，AF=CE，DF=BE，DF∥BE． 求证：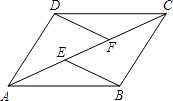
（1）△AFD≌△CEB；
（2）四边形ABCD是平行四边形．
参考答案：
【答案】
（1）证明：∵DF∥BE，
∴∠DFE=∠BEF．
又∵AF=CE，DF=BE，
∴△AFD≌△CEB（SAS）
（2）证明：由（1）知△AFD≌△CEB，
∴∠DAC=∠BCA，AD=BC，
∴AD∥BC．
∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）．
【解析】（1）利用两边和它们的夹角对应相等的两三角形全等（SAS），这一判定定理容易证明△AFD≌△CEB．（2）由△AFD≌△CEB，容易证明AD=BC且AD∥BC，可根据一组对边平行且相等的四边形是平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算（﹣x2）x3的结果是（ ）
A.x3
B.﹣x5
C.x6
D.﹣x6 -
科目： 来源： 题型：
查看答案和解析>>【题目】对于下列图形：①等边三角形；②矩形；③平行四边形；④菱形；⑤正八边形；⑥圆．其中既是轴对称图形，又是中心对称图形的是______．（填写图形的相应编号）
-
科目： 来源： 题型：
查看答案和解析>>【题目】今年4月，我市某中学举行了“爱我中国朗诵比赛”活动，根据学生的成绩划分为A、B、C、D四个等级，并绘制了如下两种不完整的统计图．根据图中提供的信息，回答下列问题：
（1）参加朗诵比赛的学生共有 ，并把条形统计图补充完整；
（2）扇形统计图中，m= ，n= ；C等级对应扇形的圆心角为 度；
（3）学校准备从获A等级的学生中随机选取2人，参加市举办的朗诵比赛，请利用列表法或树形图法，求获A等级的小明参加市朗诵比赛的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，小明在大楼30米高（即PH＝30米）的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B处的俯角为60°，已知该山坡的坡度i（即tan∠ABC）为1：
，点P、H、B、C、A在同一个平面上．点H、B、C在同一条直线上，且PH⊥HC．
（1）山坡坡角（即∠ABC）的度数等于 度；
（2）求山坡A、B两点间的距离（结果精确到0.1米）．
（参考数据：
≈1.414，
≈1.732） -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，点M是边BC的中点，AD平分∠BAC，BD⊥AD，BD的延长线交AC于点E，AB=12，AC=20．
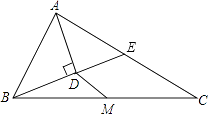
（1）求证：BD=DE；
（2）求DM的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】点P(3，－2)关于y轴的对称点的坐标是( )
A. (－3，－2) B. (3，2)
C. (－3，2) D. (－3，1)
相关试题
