【题目】如图,四边形ABCD是一个平行四边形,BE⊥CD于点E,BF⊥AD于点F, 
(1)请用图中表示的字母表示出平行线AD与BC之间的距离;
(2)若BE=2cm,BF=4cm,求平行线AB与CD之间的距离.
参考答案:
【答案】
(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵BF⊥AD,
∴BF⊥BC,
∴平行线AD与BC之间的距离是线段BF的长度
(2)解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵BE⊥CD,
∴BE⊥AB,
∴平行线AD与BC之间的距离是线段BE的长度,是2cm
【解析】(1)根据平行四边形性质得出AD∥BC,求出BF⊥BC,即可得出答案;(2)根据平行四边形性质得出CD∥AB,求出BE⊥AB,即可得出答案.
【考点精析】掌握平行线之间的距离和平行四边形的性质是解答本题的根本,需要知道两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面的式子中正确的是( )
A.3a2﹣2a2=1
B.5a+2b=7ab
C.3a2﹣2a2=2a
D.5xy2﹣6xy2=﹣xy2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P( x, y1)与Q (x, y2)分别是两个函数图象C1与C2上的任一点. 当a ≤ x ≤ b时,有-1 ≤ y1 - y2 ≤ 1成立,则称这两个函数在a ≤ x ≤ b上是“相邻函数”,否则称它们在a ≤ x ≤ b上是“非相邻函数”.

例如,点P(x, y1)与Q (x, y2)分别是两个函数y = 3x+1与y = 2x - 1图象上的任一点,当-3 ≤ x ≤ -1时,y1 - y2 = (3x + 1) - (2x - 1) = x + 2,通过构造函数y = x + 2并研究该函数在-3 ≤ x ≤ -1上的性质,得到该函数值的范围是-1 ≤ y ≤ 1,所以-1 ≤ y1 - y2 ≤ 1成立,因此这两个函数在-3 ≤ x ≤ -1上是“相邻函数”.
(1)判断函数y = 3x + 2与y = 2x + 1在-2 ≤ x≤ 0上是否为“相邻函数”,说明理由;
(2)若函数y = x2 - x与y = x - a在0 ≤ x ≤ 2上是“相邻函数”,求a的取值范围;
(3)若函数y =
 与y =-2x + 4在1 ≤ x ≤ 2上是“相邻函数”,直接写出a的最大值与最小值.
与y =-2x + 4在1 ≤ x ≤ 2上是“相邻函数”,直接写出a的最大值与最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.
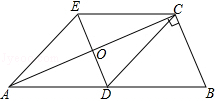
(1)求证:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求四边形ADCE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个四边形的四个内角度数的比为3∶4∶5∶6,则这个四边形的四个内角的度数分别为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究规律:如图,已知直线m∥n,A、B为直线n上的两点,C、P为直线m上的两点.
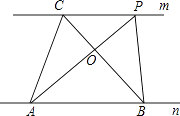
(1)请写出图中面积相等的各对三角形: .
(2)如果A、B、C为三个定点,点P在m上移动,那么无论P点移动到任何位置总有:与△ABC的面积相等;理由是: . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.
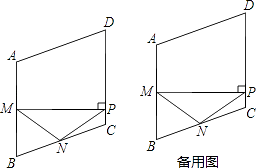
(1)若∠B=60°,这时点P与点C重合,则∠NMP=度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.
相关试题

