Question

【题目】如图，反比例函数(k≠0）与一次函数y=ax+b（a≠0）相交于点A（1，3），B（c，﹣1）．

（1）求反比例函数与一次函数的解析式；

（2）在反比例函数图象上存在点C，使△AOC为等腰三角形，这样的点有几个，请直接写出一个以AC为底边的等腰三角形顶点C的坐标．

Answer 1

【答案】（1）反比例函数解析式为y=；一次函数解析式为y=x+2；（2）C点坐标为（﹣1，﹣3）或（3，1）或（﹣3，﹣1）．

【解析】

（1）把点A（1，3）代入反比例函数的解析式即可求得k值，从而得到反比例函数的解析式；再把B（c，﹣1）代入反比例函数的解析式，求得c值，用待定系数法求一次函数的解析式即可；（2）分①以OA为腰时， AC为底、②以OA为腰时， OC为底、③以OA为底三种情况求点C的坐标即可.

（Ⅰ）∵点A（1，3）在反比例函数图象上，

∴k=1×3=3，

∴反比例函数解析式为y=；

∵B（c，﹣1）在反比例函数图象上，

∴c=﹣3，

∴B（﹣3，﹣1），

∵A、B在一次函数图象上，

∴，解得，

∴一次函数解析式为y=x+2；

（Ⅱ）当OA为腰时，若AC为底，则以O为圆心，OA为半径画圆，如图1，

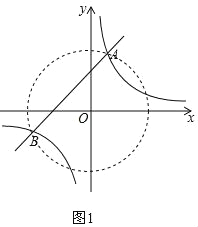
此时圆与反比例函数图象有3个交点，即满足条件的点C有三个；

若OC为底，则以A为圆心，OA长为半径画圆，如图2，

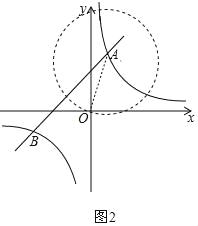
此时圆与反比例函数图象有两个交点，即满足条件的点C有两个；

当OA为底时，则点C在线段OA的垂直平分线上，如图3，

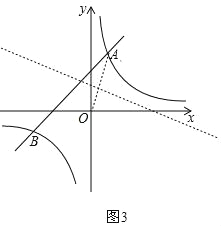
此时没有满足条件的点C；

综上可知满足条件的点C有5个；

可设C点坐标为（t，），

∵A（1，3），

∴OA2=12+32=10，OC2=t2+（）2=t2+，

当△AOC是以AC为底的等腰三角形时，则有OA=OC，即OA2=OC2，

∴10=t2+，解得t=1或t=﹣1或t=3或t=﹣3，

当t=1时，C与A重合，舍去，

∴C点坐标为（﹣1，﹣3）或（3，1）或（﹣3，﹣1）．