【题目】已知C,D两点在线段AB的垂直平分线上,且∠ACB=40°,∠ADB=68°,则∠CAD=__________.
参考答案:
【答案】126°或14°
【解析】根据中垂线的性质得出△ABC和△ADB为等腰三角形,然后求出等腰三角形底角的度数,最后分两类情况分别进行讨论得出答案.
∵点C、点D在AB的中垂线上, ∴AC=BC,AD=BD,
∵∠ACB=40°, ∴∠CAB=∠CBA=70°, ∵∠ADB=68°, ∴∠DAB=∠DBA=56°,
当点C、点D在同侧时,∠CAD=∠CAB-∠DAB=70°-56°=14°;
当点C、点D在异侧时,∠CAD=∠CAB+∠DAB=70°+56°=126°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程2x﹣4=3m和x+2=m有相同的解,则m的值是( )
A. 10 B. ﹣8 C. ﹣10 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论: ①甲船的速度是25km/h;
②从A港到C港全程为120km;
③甲船比乙船早1.5小时到达终点;
④图中P点为两者相遇的交点,P点的坐标为(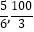 );
);
⑤如果两船相距小于10km能够相互望见,那么,甲、乙两船可以相互望见时,x的取值范围是 <x<2.
<x<2.
其中正确的结论有 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】台州某景区今年“五一”期间开始营业,为方便游客在园区内游玩休息,决定向一家园艺公司采购一批户外休闲椅,经了解,公司出售两种型号休闲椅,如下表:

景区采购这批休闲椅共用去56000元,购得的椅子正好可让1300名游客同时使用.
(1)求景区采购了多少条长条椅,多少条弧形椅?
(2)景区现计划租用A、B两种型号的卡车共20辆将这批椅子运回景区,已知A型卡车每辆可同时装运4条长条椅和11条弧形椅,B型卡车每辆可同时装运12条长条椅和7条弧形椅.如何安排A、B两种卡车可一次性将这批休闲椅运回来?
(3)又知A型卡车每辆的运费为1200元,B型卡车每辆的运费为1050元,在(2)的条件下,若要使此次运费最少,应采取哪种方案?并求出最少的运费为多少元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆锥的母线长为10,侧面展开图是半圆,则圆锥的侧面积是( )
A.100π
B.50π
C.20π
D.10π -
科目: 来源: 题型:
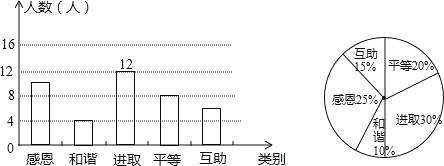
查看答案和解析>>【题目】2016年下学期,椒江某学校开展了以“责任、感恩”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下统计图表,请根据统计图表解决以下问题:
(1)该班有 人,学生选择“进取”观点的有 人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 度;
(2)如果该校有500名初三学生,利用样本估计选择“感恩”观点的初三学生约有 人;
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答).
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年国庆长假期间,“富万家”超市某商品按标价打八折销售,小玲购了一件该商品,付款56元,则该项商品的标价为_____元.
相关试题

