【题目】如图,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点E处,若∠EBC=20°,则∠EBD的度数为_________.

参考答案:
【答案】25°
【解析】易得∠DAB=110°,那么根据折叠得到∠DAB=110°,进而利用平行得到∠ABC的度数,那么就可得到∠ABA的度数,除以2就是∠ABD的度数数.
解:根据折叠的性质可得:∠ABD=∠A′BD,∠A=∠BA′D,
∵DC⊥BC,∴∠C=90°,
∵∠A′BC=20°,∴∠BA′D=∠A′BC+∠C=110°,∴∠A=110°,
∵AD∥BC,∴∠A+∠ABC=180°,
即∠A+∠ABD+∠A′BD+∠A′BC=180°,
∴110°+2∠A′BD+20°=180°,
∴∠A′BD=25°.
故答案为:25.
“点睛”本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后的角相等.
-
科目: 来源: 题型:
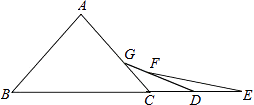
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,点D、E在BC的延长线上,G是AC上一点,且CG=CD,F是GD上一点,且DF=DE,则∠E=度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的横坐标为﹣1,点B在x轴的负半轴上,AB=AO,∠ABO=30°,直线MN经过原点O,点A关于直线MN的对称点A1在x轴的正半轴上,点B关于直线MN的对称点为B1 , 则∠AOM的度数为;点B1的纵坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将放置于直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A1OB1.已知∠AOB=30°,∠B=90°,AB=1,则B1点的坐标为( )

A. (
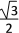 ,
, ) B. (
) B. ( ,
,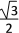 ) C. (
) C. ( ,
,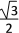 ) D (
) D (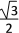 ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】若单项式2am﹣1b3与3a2bn+2同类项,则m= , n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若P(﹣3,2)与P′(3,n+1)关于原点对称,则n=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC 中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.
相关试题

