【题目】如图,在平面直角坐标系上有个点A(-1,0),点A第1次向上跳动一个单位至点A1(-1,1),紧接着第2次向右跳动2个单位至点A2(1,1),第3次向上跳动1个单位,第4次向左跳动3个单位,第5次又向上跳动1个单位,第6次向右跳动4个单位,…,依次规律跳动下去,点A第2017次跳动至点A2017的坐标是( )

A. (-504,1008) B. (-505,1009) C. (504,1009) D. (-503,1008)
参考答案:
【答案】B
【解析】试题解析:设第n次跳动至点An,
观察,发现:A(-1,0),A1(-1,1),A2(1,1),A3(1,2),A4(-2,2),A5(-2,3),A6(2,3),A7(2,4),A8(-3,4),A9(-3,5),…,
∴A4n(-n-1,2n),A4n+1(-n-1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数).
∵2017=504×4+1,
∴A2017(-504-1,504×2+1),即(-505,1009).
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】公司投资750万元,成功研制出一种市场需求量较大的产品,并再投入资金1750万元进行相关生产设备的改进.已知生产过程中,每件产品的成本为60元.在销售过程中发现,当销售单价定为120元时,年销售量为24万件;销售单价每增加10元,年销售量将减少1万件.设销售单价为x(元)(x>120),年销售量为y(万件),第一年年获利(年获利=年销售额﹣生产成本)为z(万元).
(1)求出y与x之间,z与x之间的函数关系式;
(2)该公司能否在第一年收回投资.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
【简单应用】
(2)如图2,AP、CP分别平分∠BAD.∠BCD,若∠ABC=36°,∠ADC=16°,
求∠P的度数;
【问题探究】
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.


【拓展延伸】
(4)在图4中,若设∠C=α,∠B=β,∠CAP=
 ∠CAB,∠CDP=
∠CAB,∠CDP= ∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明)
∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程x2+2x﹣k=0有两个不相等的实数根,则k的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级男生入住的一楼有x间,如果每间住6人,恰好空出一间;如果每间住5人就有4人没有房间住,则一楼共有( )间.
A. .7 B. .8 C. .9 D. 10
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有2个红球(记为红球1、红球2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=
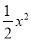 +bx﹣
+bx﹣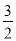 的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.(1)b= ;点D的坐标: ;
(2)线段AO上是否存在点P(点P不与A、O重合),使得OE的长为1;
(3)在x轴负半轴上是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.

相关试题

