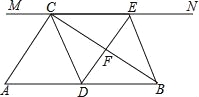
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
参考答案:
【答案】(1)证明见解析;
(2)四边形BECD是菱形;
(3)∠A=45°时,四边形BECD是正方形.
【解析】
试题分析:(1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;
(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;
(3)求出∠CDB=90°,再根据正方形的判定推出即可.
试题解析:(1)∵DE⊥BC,∴∠DFB=90°,∵∠ACB=90°,
∴∠ACB=∠DFB,∴AC∥DE,∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,∴CE=AD;
(2)四边形BECD是菱形,
理由是:∵D为AB中点,∴AD=BD,∵CE=AD,∴BD=CE,
∵BD∥CE,∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
(3)当∠A=45°时,四边形BECD是正方形,理由是:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,∴AC=BC,∵D为BA中点,∴CD⊥AB,∴∠CDB=90°,
∵四边形BECD是菱形,
∴菱形BECD是正方形,
即当∠A=45°时,四边形BECD是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:2xm2﹣12xm+18x=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标为(-2,3),点B的坐标为(-2,-3),那么点A和点B的位置关系是( )
A. 关于x轴对称 B. 关于y轴对称
C. 关于原点对称 D. 关于坐标轴和原点都不对称
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标是(4,﹣3),作点A关于x轴的对称点,得到点A′,再作点A′关于y轴的对称点,得到点A″,则点A″的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图①是一块边长为1,周长记为P1的等边三角形纸板,沿图①的底边剪去一块边长的
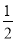 的等边三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的
的等边三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的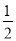 )后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1=_________
)后,得图③,④,…,记第n(n≥3)块纸板的周长为Pn,则Pn-Pn-1=_________ 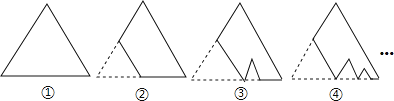
-
科目: 来源: 题型:
查看答案和解析>>【题目】若两个有理数的差是正数,那么( ).
A.被减数是正数,减数是负数;
B.被减数和减数都是正数;
C.被减数大于减数;
D.被减数和减数不能同为负数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b是两个有理数,那么a-b与a比较,必定是( ).
A.a-b>a;
B.a-b<a;
C.a-b>-a;
D.大小关系取决于b.
相关试题

