【题目】如图,以O为原点的直角坐标系中,A点的坐标为(0,1),直线x=1交x轴于点B。P为线段AB上一动点,作直线PC⊥PO,交直线x=1于点C。过P点作直线MN平行于x轴,交y轴于点M,交直线x=1于点N。
(1)当点C在第一象限时,求证:△OPM≌△PCN;
(2)当点C在第一象限时,设AP长为m,四边形POBC的面积为S,请求出S与m间的函数关系式,并写出自变量m的取值范围;
(3)当点P在线段AB上移动时,点C也随之在直线x=1上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰直角三角形的点P的坐标;如果不可能,请说明理由。

参考答案:
【答案】(1)证明见解析;
(2)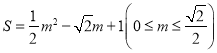
(3)使△PBC为等腰三角形的的点P的坐标为(0,1)或(![]() ,1-
,1-![]() )
)
【解析】解:(1)∵OM∥BN,MN∥OB,∠AOB=900,
∴四边形OBNM为矩形。
∴MN=OB=1,∠PMO=∠CNP=900
∵![]() ,AO=BO=1,
,AO=BO=1,
∴AM=PM。
∴OM=OA-AM=1-AM,PN=MN-PM=1-PM,
∴OM=PN, ∵∠OPC=900,
∴∠OPM+CPN=900,
又∵∠OPM+∠POM=900 ∴∠CPN=∠POM,
∴△OPM≌△PCN.
(2)∵AM=PM=APsin450= ![]() ,
,
∴NC=PM= ![]() ,∴BN=OM=PN=1-
,∴BN=OM=PN=1- ![]() ;
;
∴BC=BN-NC=1- ![]() -
- ![]() =
= ![]()
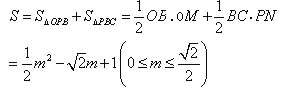
(3)△PBC可能为等腰三角形。
①当P与A重合时,PC=BC=1,此时P(0,1)
②当点C在第四象限,且PB=CB时,
有BN=PN=1-![]() , ∴BC=PB=
, ∴BC=PB=![]() PN=
PN=![]() -m,
-m,
∴NC=BN+BC=1-![]() +
+![]() -m,
-m,
由⑵知:NC=PM= ![]() ,
,
∴1-![]() +
+![]() -m=
-m= ![]() , ∴m=1.
, ∴m=1.
∴PM= ![]() =
=![]() ,BN=1-
,BN=1-![]() =1-
=1-![]() , ∴P(
, ∴P(![]() ,1-
,1-![]() ).
).
∴使△PBC为等腰三角形的的点P的坐标为(0,1)或(![]() ,1-
,1-![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校食堂厨房的桌子上整齐地摆放着若干个相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
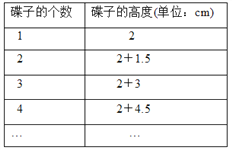
(1)若桌子上放有x个碟子,试用含x的式子,表示上述碟子的高度.下列表示碟子的高度,其中表示正确的是( )
A.1.5x+0.5 B.1.5x-0.5 C.1.5x+2 D.2x
(2)若按上述规律摆放碟子,你认为碟子的高度能达到20
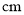 高吗?若能,请列式计算;若不能,请说明理由;
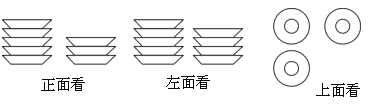
高吗?若能,请列式计算;若不能,请说明理由;(3)某天早上厨房桌上放着若干碟子,厨房李师傅分别从三个不同的方向上看,所得平面图形如下图所示,如果李师傅想把它们整齐叠成一摞,试求叠成一摞后碟子的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据﹣2、1、3、5的极差是( )
A.3B.5C.6D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】20132-2011×2015的计算结果是( )
A. 4B. -2C. 2D. -4
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年泰州市实现生产总值(GDP)5107亿元,5107亿元用科学记数法表示为_____元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】人体中红细胞的直径约为0.0000077m,将数0.0000077用科学记数法表示为( )
A.77×10﹣5
B.0.77×10﹣7
C.7.7×10﹣6
D.7.7×10﹣7 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校初三(3)班的同学踊跃为“雅安芦山地震”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但生活委员不小心把墨水滴在统计表上,部分数据看不清楚。
(1)全班有多少人捐款?
(2)如果捐款0~20元的人数在扇形统计图中所占的圆心角为72°,那么捐款21~40元的有多少人?


相关试题

