【题目】如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′E的长为( )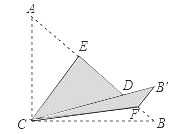
A.![]()
B.6
C.![]()
D.![]()
参考答案:
【答案】C
【解析】根据折叠的性质可知:DE=AE,∠ACE=∠DCE,∠BCF=∠B′CF,CE⊥AB,B′F=BF,
∴B′D=4-3=1,∠DCE+∠B′CF=∠ACE+∠BCF,
∵∠ACB=90°,
∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B′FC=135°,
∴∠B′FE=90°,
∵S△ABC= ![]() ACBC=
ACBC= ![]() ABCE,
ABCE,
∴ACBC=ABCE,
∵根据勾股定理得:AB= ![]() =10,
=10,
∴CE= ![]() =4.8,
=4.8,
∴EF=4.8,AE= ![]() =3.6,
=3.6,
∴B′F=BF=AB-AE-EF=10-3.6-4.8=1.6,
∴B′E= ![]() .
.
所以答案是:C.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在联欢会上,有A、B、C三名选手站在一个三角形的三个顶点位置上,他们在玩“抢凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的()
A. 三边中垂线的交点 B. 三边中线的交点
C. 三条角平分线的交点 D. 三边上高的交点
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,AC∥BD,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( )
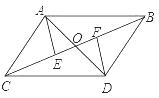
A.5对
B.6对
C.7对
D.8对 -
科目: 来源: 题型:
查看答案和解析>>【题目】若M=(a+3)(a-4),N=(a+2)(2a-5),其中a为有理数,请用所学的数学知识来比较它们的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)4x2-16=0;
(2) (x-2)3=18.
(x-2)3=18. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A. a2a4=a8 B. (a3)2=a5 C. (3ax)2=9a2x2 D. a2+a2=a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过对某校七年级学生参加课外兴趣活动情况的调查,王小华制得如下统计图,请你根据统计图,回答如下问题:
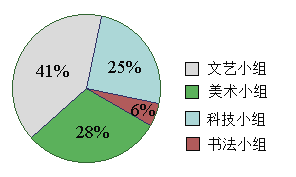
(1)哪种课外活动小组最受欢迎?
(2)哪两种课外活动小组的受欢迎程度较为接近?
(3)你还能从该统计图中获得其它信息吗?
(4)你能从统计图中计算出参加各个课外活动小组的人数吗?如果能,请计算出来.
相关试题

