【题目】如图1,有一块三角形余料ABC,它的边BC=60mm,高AD=40mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?请你计算。

变式(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图2,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
变式(2)如果原题中所要加工的零件只是一个矩形,如图3,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.

参考答案:
【答案】(1)这个矩形零件的两条边长分别为![]() mm,
mm,![]() mm;
mm;
(2)S有最大值时,PN=30mm,PQ=20mm.
【解析】试题分析:(1)设正方形的边长为xmm,则PN=PQ=ED=x,AE=AD-ED=80-x,通过证明△APN∽△ABC,利用相似比可得到![]() ,然后根据比例性质求出x即可;
,然后根据比例性质求出x即可;
(2)由于矩形是由两个并排放置的正方形所组成,则可设PQ=x,则PN=2x,AE=40-x,然后与(1)的方法一样求解;(3)设PN=x,用PQ表示出AE的长度,然后根据相似三角形对应高的比等于相似比列出比例式并用x表示出PN,然后根据矩形的面积公式列式计算,再根据二次函数的最值问题解答.
试题解析:(1)如图1,设正方形的边长为xmm,则PN=PQ=ED=x,∴AE=ADED=40x,∵PN∥BC,
∴△APN∽△ABC,
∴![]() ,即
,即![]() ,
,
解得x=24.
∴加工成的正方形零件的边长是24mm;
(2)如图2,设PQ=x,则PN=2x,AE=40x,
∵PN∥BC,
∴△APN∽△ABC,
∴![]() ,即
,即![]() ,
,
解得:x=![]() ,
,
∴2x=![]() ,
,
∴这个矩形零件的两条边长分别为![]() mm,
mm, ![]() mm;
mm;
(3)如图3,设PN=x(mm),矩形PQMN的面积为S(mm2),
由条件可得△APN∽△ABC,
∴![]() ,即
,即![]() ,
,
解得:PQ=![]() .
.
则S=PNPQ=x(![]() )=
)=![]() x2+40x=
x2+40x=![]() (x30)2+600,
(x30)2+600,
故S的最大值为600mm2,此时PN=30mm,PQ=40![]() ×30=20(mm).
×30=20(mm).
-
科目: 来源: 题型:
查看答案和解析>>【题目】自然数4,5,5,x,y从小到大排列后,其中位数为4,如果这组数据唯一的众数是5,那么,所有满足条件的x,y中,x+y的最大值是( )
A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】将式子3﹣5﹣7写成和的形式,正确的是( )
A.3+5+7
B.﹣3+(﹣5)+(﹣7)
C.3﹣(+5)﹣(+7)
D.3+(﹣5)+(﹣7) -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】派派的妈妈和派派今年共36岁,再过5年,派派的妈妈的年龄比派派年龄的4倍还大1岁,当派派的妈妈40岁时,则派派的年龄为_____岁.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一水管向某容器内持续注水,设单位时间内注入的水量保持不变;在注水过程中,表示容器内水深h与注水时间t的关系有如图所示的A,B,C,D四个图象,它们分别与E,F,G,H四种容器中的其中一种相对应,请你把相对应容器的字母填在下面的横线上.
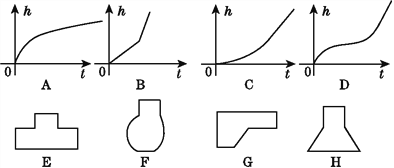
A→____________;B→____________;C→____________;D→____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明用自制的直角三角形纸板DEF测量树AB的高度,他调整自己的位置,使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40 cm,EF=20 cm,测得边DF离地面的高度AC=1.5 m, CD=10 m,请你帮小明求下树的高度。
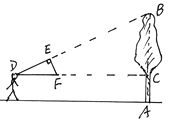
相关试题

