【题目】如图1,对称轴为直线x= ![]() 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A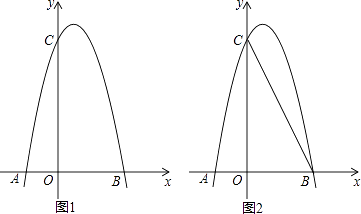
(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:由对称性得:A(﹣1,0),
设抛物线的解析式为:y=a(x+1)(x﹣2),
把C(0,4)代入:4=﹣2a,
a=﹣2,
∴y=﹣2(x+1)(x﹣2),
∴抛物线的解析式为:y=﹣2x2+2x+4;
(2)解:如图1,设点P(m,﹣2m2+2m+4),过P作PD⊥x轴,垂足为D,

∴S=S梯形+S△PDB= ![]() m(﹣2m2+2m+4+4)+
m(﹣2m2+2m+4+4)+ ![]() (﹣2m2+2m+4)(2﹣m),
(﹣2m2+2m+4)(2﹣m),
S=﹣2m2+4m+4=﹣2(m﹣1)2+6,
∵﹣2<0,
∴S有最大值,则S大=6;
(3)解:存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形,
理由是:
分以下两种情况:
①当∠BQM=90°时,如图2:
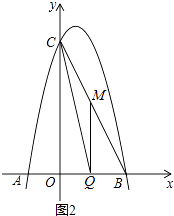
∵∠CMQ>90°,
∴只能CM=MQ.
设直线BC的解析式为:y=kx+b(k≠0),
把B(2,0)、C(0,4)代入得: ![]() ,
,
解得: ![]() ,
,
∴直线BC的解析式为:y=﹣2x+4,
设M(m,﹣2m+4),
则MQ=﹣2m+4,OQ=m,BQ=2﹣m,
在Rt△OBC中,BC= ![]() =
= ![]() =2
=2 ![]() ,
,
∵MQ∥OC,
∴△BMQ∽BCO,
∴ ![]() ,即
,即 ![]() ,
,
∴BM= ![]() (2﹣m)=2
(2﹣m)=2 ![]() ﹣
﹣ ![]() m,
m,
∴CM=BC﹣BM=2 ![]() ﹣(2
﹣(2 ![]() ﹣
﹣ ![]() m)=
m)= ![]() m,
m,
∵CM=MQ,
∴﹣2m+4= ![]() m,m=
m,m= ![]() =4
=4 ![]() ﹣8.
﹣8.
∴Q(4 ![]() ﹣8,0).
﹣8,0).
②当∠QMB=90°时,如图3,
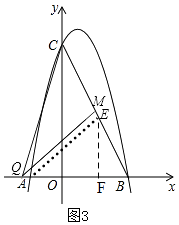
同理可设M(m,﹣2m+4),
过A作AE⊥BC,垂足为E,
∴∠EAB=∠OCB,
∴sin∠EAB= ![]() ,
,
∴ ![]() ,
,
∴BE= ![]() ,
,
过E作EF⊥x轴于F,
sin∠CBO= ![]() ,
,
∴ ![]() ,
,
∴EF= ![]() ,
,
由勾股定理得:BF= ![]() =
= ![]() ,
,
∴OF=2﹣ ![]() =
= ![]() ,
,
∴E( ![]() ,
, ![]() ),
),
由A(﹣1,0)和E( ![]() ,
, ![]() )可得:
)可得:
则AE的解析式为:y= ![]() x+
x+ ![]() ,
,
则直线BC与直线AE的交点E(1.4,1.2),
设Q(﹣x,0)(x>0),
∵AE∥QM,
∴△ABE∽△QBM,
∴ ![]() ①,
①,
由勾股定理得:x2+42=2×[m2+(﹣2m+4﹣4)2]②,
由以上两式得:m1=4(舍),m2= ![]() ,
,
当m= ![]() 时,x=
时,x= ![]() ,
,
∴Q(﹣ ![]() ,0).
,0).
综上所述,Q点坐标为(4 ![]() ﹣8,0)或(﹣
﹣8,0)或(﹣ ![]() ,0).
,0).
【解析】(1)首先依据点A与点B关于x=![]() 对称求得点A的坐标,然后利用待定系数法求求得抛物线的解析式即可;
对称求得点A的坐标,然后利用待定系数法求求得抛物线的解析式即可;
(2)设点P(m,﹣2m2+2m+4),过P作PD⊥x轴,垂足为D,然后得到S与m的函数关系式,接下来,依据二次函数的性质求得S的最大值即可;
(3)分为∠BQM=90°和∠QMB=90°两种情况画出图像,当∠BQM=90°时,先证明△BMQ∽BCO,然后再依据相似三角形的性质列方出求解即可;当∠QMB=90°时,过A作AE⊥BC,垂足为E,过E作EF⊥x轴于F,然后证明△ABE∽△QBM,然后再依据似三角形的性质列方出求解即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,FG∥EB,∠2=∠3,那么∠EDB+∠DBC等于多少度?为什么?

解:因为FG∥EB(已知),
所以
 (__________).
(__________).因为
 (已知),
(已知),所以
 (___________).
(___________).所以DE∥BC (__________).
所以
 ______(__________).
______(__________). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( )
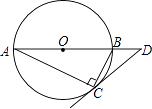
A.25°
B.40°
C.50°
D.65° -
科目: 来源: 题型:
查看答案和解析>>【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】细心观察图,认真分析各式,然后解答问题:
 ;
; ;
; ;
;

(1)请用含
 (
( 为正整数)的等式表示上述交化规律:______;
为正整数)的等式表示上述交化规律:______;(2)观察总结得出结论:直角三角形两条直角边与斜边的关系,用一句话概括为:______;
(3)利用上面的结论及规律,请在图中作出等于
 的长度;
的长度;(4)若
 表示三角形面积,
表示三角形面积, ,
, ,
,
 ,计算出
,计算出 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广,为响应号召,某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
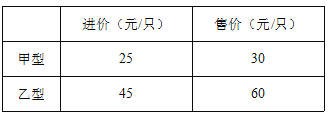
(1)如何进货,进货款恰好为46000元?
(2)设商场购进甲种节能灯x只,求出商场销售完节能灯时总利润w与购进甲种节能灯x之间的函数关系式;
(3)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时利润为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四个完全相同的小球上分别写上1,2,3,4四个数字,然后装入一个不透明的口袋内搅匀,从口袋内取出一个球记下数字后作为点P的横坐标x,放回袋中搅匀,然后再从袋中取出一个球记下数字后作为点P的纵坐标y,则点P(x,y)落在直线y=﹣x+5上的概率是 .
相关试题

