Question

【题目】阅读理解：对于任意正实数a、b，∵（）2≥0，∴a-2，∴a+b≥2，当且仅当a=b时，等号成立．

结论：在a+b（a、b均为正实数）中，若ab为定值P，则a+b，

当且仅当a=b时，a+b有最小值．

根据上述内容，回答下列问题：

（1）若x＞0，只有当x= 时，4x+有最小值为 ．

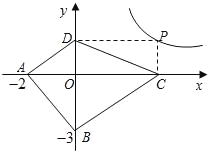
（2）探索应用：如图，已知A（-2，0），B（0，-3），点P为双曲线y=（x＞0）上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D，求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．

（3）已知x＞0，则自变量x为何值时，函数y=取到最大值，最大值为多少？

Answer 1

【答案】（1），12；（2）最小值为12，四边形ABCD是菱形；（3）．

【解析】

试题分析：（1）直接利用a+b≥2，当且仅当a=b时，等号成立；求解即可求得答案；

（2）首先设P（x，），则C（x，0），D（0，），可得S四边形ABCD=ACBD=（x+2）（+3），然后利用a+b≥2，当且仅当a=b时，等号成立求解即可求得答案；

（3）首先将原式变形为y==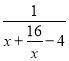，继而求得答案．

试题解析：（1）∵4x+≥2×=12，当且仅当4x=时，等号成立，

∵x＞0，

∴x=，

∴若x＞0，只有当x=时，4x+有最小值为12；

（2）设P（x，），则C（x，0），D（0，），

∴BD=+3，AC=x+2，

∴S四边形ABCD=ACBD=（x+2）（+3）=6+x+≥6+2=12，

当且仅当x=，即x=2时，四边形ABCD面积的最小值为12，

∴OB=OD=3，OA=OC=2，

∴四边形ABCD是平行四边形，

∵AC⊥BD，

∴四边形ABCD是菱形；

（3）∵x＞0，

∴y==≤，

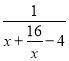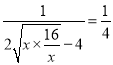当且仅当x=，即x=4时，函数y=取到最大值，最大值为：．