【题目】在△ABC中,AB=AC,D为射线BA上一点,连接DC,且DC=BC.
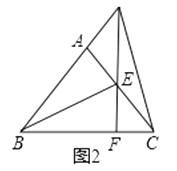
(1)如图1,若DC⊥AC,AB= ![]() ,求CD的长;
,求CD的长;
(2)如图2,若E为AC上一点,且CE=AD;连接BE,BE=2CE,连接DE并延长交BC于F.求证:DF=3EF.
参考答案:
【答案】
(1)解:∵AB=AC,BC=DC
∴∠B=∠ACB,∠B=∠D,
∴∠ACB=∠D=∠B 又∵DC⊥AC,
∴∠ACD=90°
∴∠B+∠ACB+∠D=90°∴∠B=∠ACD=∠D=30°
∵AB= ![]() ,
,
∴AC= ![]() ,
,
∴CD= ![]() AC=
AC= ![]() .
.
(2)解:证明:∵AB=AC,BC=DC
∴∠ABC=∠ACB,∠ABC=∠CDA
∴∠BCE=∠CDA 又∵BC=DC,CE=DA,
∴△BCE≌△DCA,
∴CE=AD,BE=AC
又∵BE=2CE,
∴AE=CE,AD=AE,过A作AH⊥DF于H,则∠DAH=∠HAE,DH=EH,
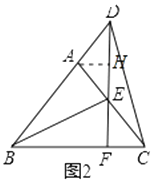
又∵∠DAC=∠ABC+∠ACB=2∠ACB,
∴∠HAE=∠ACB,
又∵∠AEH=∠CEF,AE=CE,
∴△AEH≌△CEF,
∴EH=EF,
∴DH=EH=EF,即DF=3EF
【解析】(1)由AB=AC,BC=DC,可得∠B=∠ACB,∠B=∠D,又DC⊥AC,可得∠B=∠ACD=∠D=30°,再由30度角的正切可得CD= ![]() AC= 6;(2)由已知易证△BCE≌△DCA,可得AE=CE,再由AD=AE,AH⊥DF,可得,DH=EH,进而须证HE=EF,因此证出EH=EF即可.
AC= 6;(2)由已知易证△BCE≌△DCA,可得AE=CE,再由AD=AE,AH⊥DF,可得,DH=EH,进而须证HE=EF,因此证出EH=EF即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图放置的△OAB1 , △B1A1B2 , △B2A2B3 , …都是边长为2的等边三角形,点A在y轴上,点O,B1 , B2 , B3…都在直线l上,则点B2017的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】邵阳县某校为了了解学生对语文(A)、数学(B)、英语(C)、物理(D)四科的喜爱程度(每人只选一科),特对八年级某班进行了调查,并绘制成如下频数和频率统计表和扇形统计图.


(1)求出这次调查的总人数;
(2)求出表中a、b、c、d的值;
(3)若该校八年级有学生1000人,请你算出喜爱英语的人数,并发表你的看法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是AB上任一点,∠ABC=∠ABD,从下列各条件中补充一个条件,不一定能推出ΔAPC≌ΔAPD.的是( )

A. BC=BD. B. ∠ACB=∠ADB. C. ∠CAB=∠DAB D. AC=AD.
-
科目: 来源: 题型:
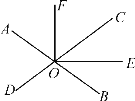
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE是∠COB的平分线,∠FOE=90°,若∠AOD=70°.
(1)求∠BOE的度数;
(2)OF是∠AOC的平分线吗?请说明理由.
-
科目: 来源: 题型:
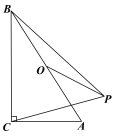
查看答案和解析>>【题目】在Rt△ACB中,C为直角顶点,∠ABC=25°,O为斜边AB的中点,将OA绕着点O逆时针旋转α(0°<α<180°)到OP.当△BCP为等腰三角形时,α的度数为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】厦深铁路开通后,直线l1与l2分别表示从深圳北开往潮阳站的动车和从潮阳站开往深圳的高铁,两车同时出发,设动车离深圳北的距离为y1(千米),高铁离深圳的距离为距离y2(千米),行驶时间为t(小时),与t的函数关系如图所示:
(1)高铁的速度为 km/h;
(2)动车的速度为 km/h;
(3)动车出发多少小时与高铁相遇?
(4)两车出发经过多长时间相距50千米?

相关试题

