【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C. 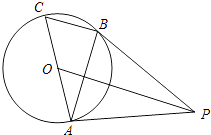
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ![]() ,求BC的长.
,求BC的长.
参考答案:
【答案】
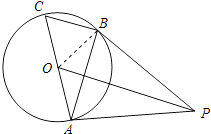
(1)证明:连接OB,如图所示:
∵AC是⊙O的直径,
∴∠ABC=90°,
∴∠C+∠BAC=90°,
∵OA=OB,
∴∠BAC=∠OBA,
∵∠PBA=∠C,
∴∠PBA+∠OBA=90°,
即PB⊥OB,
∴PB是⊙O的切线
(2)解:∵⊙O的半径为2 ![]() ,
,
∴OB=2 ![]() ,AC=4
,AC=4 ![]() ,
,
∵OP∥BC,
∴∠C=∠BOP,
又∵∠ABC=∠PBO=90°,
∴△ABC∽△PBO,
∴ ![]() ,
,
即 ![]() ,
,
∴BC=2
【解析】(1)连接OB,由圆周角定理得出∠ABC=90°,得出∠C+∠BAC=90°,再由OA=OB,得出∠BAC=∠OBA,证出∠PBA+∠OBA=90°,即可得出结论;(2)证明△ABC∽△PBO,得出对应边成比例,即可求出BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=300,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.其中正确结论的序号是( )

A. ②④ B. ①③ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励居民节约用水,某市自来水公司对每户月用水量进行计费,每户每月用水量在规定吨数以下的收费标准相同;规定吨数以上的超过部分收费标准相同,以下是小明家
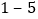 月份用水量和交费情况:
月份用水量和交费情况:月份
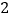
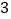
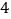
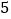
用水量(吨)
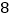
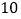
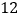
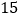
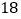
费用(元)
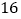
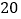
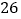

根据表格中提供的信息,回答以下问题:
 求出规定吨数和两种收费标准;
求出规定吨数和两种收费标准;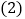 若小明家
若小明家 月份用水
月份用水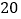 吨,则应缴多少元?
吨,则应缴多少元?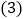 若小明家
若小明家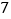 月份缴水费
月份缴水费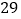 元,则
元,则 月份用水多少吨?
月份用水多少吨? -
科目: 来源: 题型:
查看答案和解析>>【题目】某工程,甲工程队单独做40天完成,若乙工程队单独做30天后,甲、乙两工程队再合作20天完成。
(1)(5分)求乙工程队单独做需要多少天完成?
(2)(4分)将工程分两部分,甲做其中一部分用了x天,乙做另一部分用了y天,其中x、y均为正整数,且x<15,y<70,求x、y.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某月的月历,用带阴影的方框任意框九个数。
(1)图中带阴影的方框中的9个数之和与方框正中心的数有什么关系?请说明你的理由?
(2)若这9个数之和是81,你能说出这9个日期吗?只要回答能或不能,且说明为什么?
(3)这9个数之和可能会是100吗?如果可能,请计算出这9个日期,如果不可能,请说明为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字.
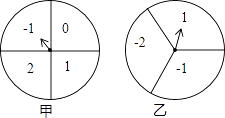
(1)直接写出转动甲盘停止后指针指向数字“1”的概率;
(2)小华和小明利用这两个转盘做游戏,两人分别同时转动甲、乙两个转盘,停止后,指针各指向一个数字,若两数字之积为非负数则小华胜;否则,小明胜.你认为这个游戏公平吗?请你利用列举法说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小兰画了一个函数y=x2+ax+b的图象如图,则关于x的方程x2+ax+b=0的解是( )

A.无解
B.x=1
C.x=﹣4
D.x=﹣1或x=4
相关试题

