【题目】阅读与应用:阅读1:a、b为实数,且a>0,b>0,因为![]() ,所以
,所以![]() 从而
从而![]() (当a=b时取等号).
(当a=b时取等号).
阅读2:若函数![]() ;(m>0,x>0,m为常数),由阅读1结论可知:
;(m>0,x>0,m为常数),由阅读1结论可知:![]() ,所以当
,所以当![]() ,即
,即![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() .
.
阅读理解上述内容,解答下列问题:
问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为![]() ,周长为2(
,周长为2(![]() ),求当x= 时,周长的最小值为 ;
),求当x= 时,周长的最小值为 ;
问题2:已知函数![]() (
(![]() )与函数
)与函数![]() (
(![]() ),
),
当x= 时,![]() 的最小值为 ;
的最小值为 ;
问题3:某民办学校每天的支出总费用包含以下三个部分:一是教职工工资4900元;二是学生生活费成本每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)
参考答案:
【答案】(1)2,8;(2)2,6;(3)700,24.
【解析】
试题分析:问题1:由阅读2得到![]() 的范围,进一步得到周长的最小值;
的范围,进一步得到周长的最小值;
问题2:把![]() 变形为
变形为![]() ,由阅读2得到
,由阅读2得到![]() 的范围,进一步即可求解;
的范围,进一步即可求解;
问题3:可设学校学生人数为x人,根据生均投入=支出总费用÷学生人数,列出代数式,再由阅读2得到范围,从而求解.
试题解析:问题1:![]() (
(![]() ),解得x=2,x=2时,
),解得x=2,x=2时,![]() 有最小值为
有最小值为![]() =4.故当x=2时,周长的最小值为2×4=8;
=4.故当x=2时,周长的最小值为2×4=8;
问题2:∵![]() (
(![]() ),
),![]() (
(![]() ),∴
),∴![]() =
=![]() ,
,![]() ,解得x=2,x=2时,
,解得x=2,x=2时,![]() 有最小值为
有最小值为![]() =6;
=6;
问题3:设学校学生人数为x人,则生均投入=![]() =
=![]() =
=![]() ,
,![]() (
(![]() ),解得x=700,x=700时,
),解得x=700,x=700时,![]() 有最小值为
有最小值为![]() =1400,故当x=700时,生均投入的最小值为10+0.01×1400=24元.
=1400,故当x=700时,生均投入的最小值为10+0.01×1400=24元.
答:当学校学生人数为700时,该校每天生均投入最低,最低费用是24元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示0.0000907= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC于D,AE平分∠DAC,∠BAC=80°,∠B=60°,求∠AEC的度数.
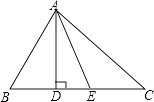
-
科目: 来源: 题型:
查看答案和解析>>【题目】据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示应为( )
A.0.3×106
B.3×105
C.3×106
D.30×104 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了表示某种食品中钙、维生素、糖等物质的含量的百分比,应选用( )
A. 条形统计图 B. 折线统计图
C. 扇形统计图 D. 直方图
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并解决相关的问题.
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1 , 依此类推,排在第n位的数称为第n项,记为an .
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0).如:数列1,2,4,8,…为等比数列,其中a1=1,公比为q=2.
则:
(1)等比数列3,6,12,…的公比q为 , 第6项是 .
(2)如果一个数列a1 , a2 , a3 , a4 , …是等比数列,且公比为q,那么根据定义可得到: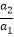 =q,
=q, 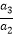 =q,
=q, 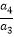 =q,…
=q,… 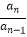 =q.
=q.
所以:a2=a1q,a3=a2q=(a1q)q=a1q2 , a4=a3q=(a1q2)q=a1q3 , …
由此可得:an=(用a1和q的代数式表示).
(3)对等比数列1,2,4,…,2n﹣1求和,可采用如下方法进行:
设S=1+2+4+…+2n﹣1 ①,
则2S=2+4+…+2n ②,
②﹣①得:S=2n﹣1
利用上述方法计算:1+3+9+…+3n . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( )
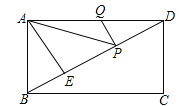
A.
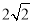 B.
B.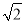 C.
C.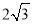 D.
D.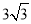
相关试题

