【题目】已知,如图,直线AB、CD、EF都经过点O,且AB⊥CD,OG平分∠BOE,如果∠EOG= ![]() ∠AOE,求∠EOG和∠DOF的度数.
∠AOE,求∠EOG和∠DOF的度数. 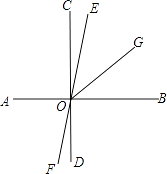
参考答案:
【答案】解:∵OG平分∠BOE,
∴∠EOG=∠BOG,
设∠AOE=x°,
∴∠EOG=∠GOB= ![]() x°,
x°,
∴x+ ![]() x+
x+ ![]() x=180,
x=180,
解得:x=100,
∴∠EOG=100°× ![]() =40°,
=40°,
∵AB⊥CD,
∴∠BOC=90°,
∴∠DOF=∠COE=90°﹣40°﹣40°=10°
【解析】首先根据角平分线的性质可得∠EOG=∠BOG,设∠AOE=x°,进而得到∠EOG=∠GOB= ![]() x°,再根据平角为180°可得x+
x°,再根据平角为180°可得x+ ![]() x+
x+ ![]() x=180,解出x可得∠EOG,进而可得∠DOF的度数.
x=180,解出x可得∠EOG,进而可得∠DOF的度数.
【考点精析】根据题目的已知条件,利用角的平分线和对顶角和邻补角的相关知识可以得到问题的答案,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是( )
A. 对角线互相平分的四边形是平行四边形
B. 两组对边分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形
D. 一组对边相等,另一组对边平行的四边形是平行四边形
-
科目: 来源: 题型:
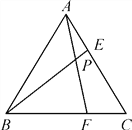
查看答案和解析>>【题目】如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P,且AE=CF.
(1)求证:AF=BE,并求∠FPB的度数;
(2)若AE=2,试求AP·AF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式﹣2x<4的解集是( )
A. x>2 B. x<2 C. x<﹣2 D. x>﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. 3a2+a2=4a4 B. (a2)3=a5 C. a·a2=a3 D. (2a)3=6a3
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据3、3、5、8、11的中位数是( )
A. 3B. 4C. 5D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校校门口有一个长为9m的长条形(长方形)电子显示屏,学校的有关活动都会在“电子显示屏”播出,由于各次活动的名称不同,字数也就不等,为了制作及显示时方便美观,负责播出的老师对有关数据作出了如下规定:若字数在8个以下,边空:字宽:字距=2:4:1;若字数在8个以上(含8个),边空:字宽:字距=2:3:1,如图所录:

(1)某次活动的字数为9个,求字距是多少?
(2)如果某次活动的字宽为36cm,问字数是多少个?
相关试题

