【题目】如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到![]() .
.
(1)线段![]() 的长是 ,∠AOB1的度数是 ;
的长是 ,∠AOB1的度数是 ;
(2)连接![]() ,求证:四边形
,求证:四边形![]() 是平行四边形;
是平行四边形;
(3)求四边形![]() 的面积.
的面积.

参考答案:
【答案】(1)6;135°;(2)证明详见解析;(3)36.
【解析】
试题分析:(1)图形在旋转过程中,边长和角的度数不变;
(2)可证明OA∥![]() 且相等,即可证明四边形
且相等,即可证明四边形![]() 是平行四边形;
是平行四边形;
(3)平行四边形的面积=底×高=OA×![]() .
.
试题解析:(1)解:因为∠OAB=90°,OA=AB,
所以△OAB为等腰直角三角形,即∠AOB=45°,
根据旋转的性质,对应点到旋转中心的距离相等,即![]() =OA=6,
=OA=6,
对应角∠![]() =∠AOB=45°,旋转角∠
=∠AOB=45°,旋转角∠![]() =90°,
=90°,
所以∠![]() 的度数是90°+45°=135°.
的度数是90°+45°=135°.
故答案为:6;135°;
(2)证明:∵∠![]() =∠
=∠![]() =90°,
=90°,
∴OA∥![]() ,
,
又∵OA=AB=![]() ,
,
∴四边形![]() 是平行四边形;
是平行四边形;
(3)平行四边形![]() 的面积=6×6=36.
的面积=6×6=36.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数a,b,我们定义符号max{a,b}的意义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b]=b;如:max{4,﹣2}=4,max{3,3}=3,若关于x的函数为y=max{x+3,﹣x+1},则该函数的最小值是( )
A. 0 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校组织的社会实践活动中,甲、乙两人参加了射击比赛,每人射击七次,命中的环数如下表所示:
甲(环)
7
8
8
6
9
8
10
乙(环)
5
10
6
7
8
10
10
根据以上信息,解决下列问题:
(1)写出甲、乙两人命中环数的众数;
(2)已知通过计算求得
 =8,
=8,  ≈1.43,试比较甲、乙两人谁的成绩更稳定?
≈1.43,试比较甲、乙两人谁的成绩更稳定? -
科目: 来源: 题型:
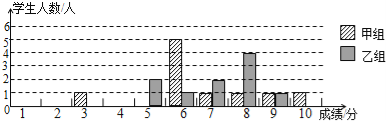
查看答案和解析>>【题目】某校团委举办了一次“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上为合格,达到9分以上(含9分)为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如下.
(1)补充完成下列的成绩统计分析表:
组别
平均分
中位数
方差
合格率
优秀率
甲
6.7
3.41
90%
20%
乙
7.5
80%
10%
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程3x+a=0的解比方程2x﹣3=x+5的解大2,求a值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
13=12
13+23=32
13+23+33=62
13+23+33+43=102…
(1)根据观察得到规律写出:13+23+33+43+53═ .
(2)根据观察得到规律写出13+23+33+43+…+1003= .
(3)13+23+33+43+53+…+n3= -
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
选手
表达能力
阅读理解
综合素质
汉字听写
甲
85
78
85
73
乙
73
80
82
83
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
相关试题

