【题目】如图,在△ABC中,点E,F在BC上,EM垂直平分AB交AB于点M,FN垂直平分AC交AC于点N,∠EAF=90°,BC=12,EF=5.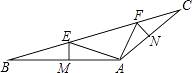
(1)求∠BAC的度数;
(2)求S△EAF .
参考答案:
【答案】
(1)解:∵EM垂直平分AB,
∴AE=BE,
∴∠B=∠BAE.
∵FN垂直平分AC,
∴AF=EC
∴∠C=∠CAF.
∵∠B+∠BAE+∠EAF+∠C+∠CAF=180°,∠EAF=90°,
∴2∠BAE+2∠CAF=90°,
∴∠BAE+∠CAF=45°,
∴∠BAC=∠BEA+∠EAF+∠CAF=45°+90°=135°
(2)解:∵EM垂直平分AB,
∴EB=EA.
∵FN垂直平分AC,
∴FA=FC.
∵BC=12,EF=5,
∴EA+FA=12﹣5=7.
∵EF=5,∠EAF=90°,
∴EA2+FA2=(EA+FA)2﹣2EAFA=EF2=25,
∴ ![]() EAFA=6,
EAFA=6,
∴S△EAF=6
【解析】(1)根据垂直平分线上的点到线段两端点的距离相等,得出AE=BE、AF=EC,证出∠B=∠BAE.∠C=∠CAF,再在△ABC中,利用三角形内角和定理及∠EAF=90°,证出∠BAE+∠CAF=45°,从而可求出∠BAC的度数。
(2)根据AB、EF的长求出BE+FC的长,即可得到EA+FA=7,再根据勾股定理得出EA2+FA2=EF2=25,两式结合求出EAFA的值,再利用三角形的面积公式求出△EAF的面积即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件是必然事件的是( )
A.明天太阳从西方升起
B.打开电视机,正在播放广告
C.掷一枚硬币,正面朝上
D.任意一个三角形,它的内角和等于180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线
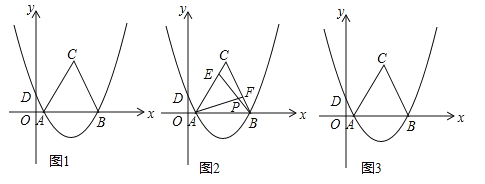
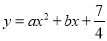 ,经过A(1,0)、B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边△ABC.
,经过A(1,0)、B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边△ABC.(1)求抛物线的解析式;
(2)在x轴上方的抛物线上是否存在点M,是S△ABM=
 S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;(3)如图2,E是线段AC上的动点,F是线段BC上的动点,AF与BE相交于点P.
①若CE=BF,试猜想AF与BE的数量关系及∠APB的度数,并说明理由;
②若AF=BE,当点E由A运动到C时,请直接写出点P经过的路径长(不需要写过程).
-
科目: 来源: 题型:
查看答案和解析>>【题目】近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A,B两种型号的空气净化器,两种净化器的销售相关信息见下表:
A型销售数量(台)
B型销售数量(台)
总利润(元)
5
10
2 000
10
5
2 500
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300 m3/小时,B型空气净化器的净化能力为200 m3/小时.某长方体室内活动场地的总面积为200 m2,室内墙高3 m.该场地负责人计划购买5台空气净化器每天花费30分钟将室内空气净化一新,如不考虑空气对流等因素,至少要购买A型空气净化器多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣4的顶点坐标是( )
A.(0,﹣4)B.(0,4)C.(2,0)D.(﹣2,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:2m2﹣(5﹣3m2+7m)+2(3m﹣2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,点M、N分别是射线OA、OB上的动点,OP平分∠AOB,且OP=6,△PMN的周长最小值为 .
相关试题

