【题目】如图,在□ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.
(1)求证:△AEB≌△CFD;
(2)若四边形EBFD是菱形,求∠ABD的度数.

参考答案:
【答案】(1)、证明过程见解析;(2)、90°
【解析】试题分析:(1)、根据平行四边形的性质和已知条件证明即可;(2)、由菱形的性质可得:BE=DE,因为∠EBD+∠EDB+∠A+∠ABE=180°,所以∠ABD=∠ABE+∠EBD=![]() ×180°=90°,问题得解.
×180°=90°,问题得解.
试题解析:(1)、∵四边形ABCD是平行四边形, ∴∠A=∠C,AD=BC,AB=CD.
∵点E、F分别是AD、BC的中点, ∴AE=![]() AD,FC=
AD,FC=![]() BC. ∴AE=CF.
BC. ∴AE=CF.
∴△AEB≌△CFD(SAS).
(2)、∵四边形EBFD是菱形, ∴BE=DE. ∴∠EBD=∠EDB. ∵AE=DE, ∴BE=AE.
∴∠A=∠ABE. ∵∠EBD+∠EDB+∠A+∠ABE=180°, ∴∠ABD=∠ABE+∠EBD=![]() ×180°=90°.
×180°=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB, OE平分∠AOC, OF平分∠BOC.
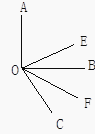
(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数;
(2)猜想∠EOF与∠AOB的数量关系;
(3)若∠AOB+∠EOF=156°,则∠EOF是多少度? -
科目: 来源: 题型:
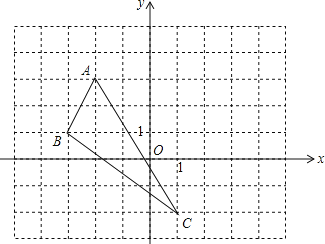
查看答案和解析>>【题目】画图题
(1)请在图中作出△ABC关于y轴的轴对称图形△A′B′C′(A,B,C的对称点分别是A′,B′,C′);
(2)直接写出△A′B′C′三点的坐标:A′(_______),B′(_______),C′(_______).
(3)求△A′B′C′的面积.
-
科目: 来源: 题型:
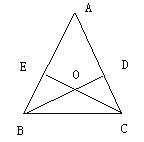
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,BD、CE是高并交于点O.
求证:(1)BD=CE;(2)OB=OC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣3πxy2z3的系数是 , 次数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3、﹣2、﹣1、4、5中任取两个数相加,若所得的和的最大值是a,最小值是b,则a+b的值是( )
A. ﹣2 B. ﹣3 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,管中放置着三根同样的绳子AA1、BB1、CC1;
(1)小明从这三根绳子中随机选一根,恰好选中绳子AA1的概率是多少?
(2)小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.

相关试题

