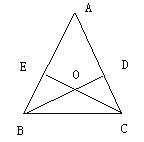
【题目】已知:如图,在△ABC中,AB=AC,BD、CE是高并交于点O.
求证:(1)BD=CE;(2)OB=OC.
参考答案:
【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)利用面积可建立等式![]() ,根据AB=AC即可得出BD=CE;(2)欲证OB=OC,可证∠OBC=∠OCB,只要证明△BEC≌△CDB即可;由已知可得∠BEC=∠CDB=90°,BD=CE,BC是公共边,即可证得.
,根据AB=AC即可得出BD=CE;(2)欲证OB=OC,可证∠OBC=∠OCB,只要证明△BEC≌△CDB即可;由已知可得∠BEC=∠CDB=90°,BD=CE,BC是公共边,即可证得.
证明:(1)∵AB=AC,且BD、CE是高,
∴![]() ,
,
∴BD=CE.
(2)∵CE⊥AB,BD⊥AC,
∴△EBC和△DCB都是直角三角形,
在Rt△EBC与Rt△DCB中,
![]() ,
,
∴Rt△EBC≌Rt△DCB(HL),
∴∠BCE=∠CBD,
∴OB=OC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某天的最高气温是6℃,最低气温是﹣2℃,那么当天的日温差是℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB, OE平分∠AOC, OF平分∠BOC.
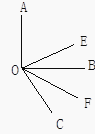
(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数;
(2)猜想∠EOF与∠AOB的数量关系;
(3)若∠AOB+∠EOF=156°,则∠EOF是多少度? -
科目: 来源: 题型:
查看答案和解析>>【题目】画图题
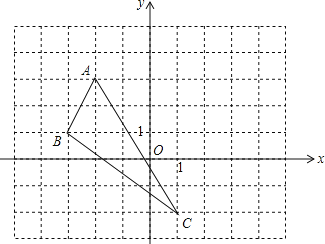
(1)请在图中作出△ABC关于y轴的轴对称图形△A′B′C′(A,B,C的对称点分别是A′,B′,C′);
(2)直接写出△A′B′C′三点的坐标:A′(_______),B′(_______),C′(_______).
(3)求△A′B′C′的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.
(1)求证:△AEB≌△CFD;
(2)若四边形EBFD是菱形,求∠ABD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣3πxy2z3的系数是 , 次数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3、﹣2、﹣1、4、5中任取两个数相加,若所得的和的最大值是a,最小值是b,则a+b的值是( )
A. ﹣2 B. ﹣3 C. 3 D. 4
相关试题

