【题目】如图,已知△ABC中,∠B=∠C,AB=16厘米,BC=12厘米,点D为AB的中点.如果点P在线段BC上以每秒4厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).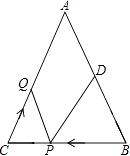
(1)用的代数式表示PC的长度;
(2)若点P、Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(3)若点P、Q的运动速度不相等,当点Q的运动速度a为多少时,能够使△BPD与△CQP全等?
参考答案:
【答案】
(1)
解:PC=BC﹣PB=12﹣4t
(2)
解:经过1秒后,△BPD与△CQP全等.
∵AB=16,点D为AB的中点,
∴BD=8,
经过1秒后,BP=CQ=4,
∵BC=12,BP=4,
∴CP=8,
∴CP=BD,
在△BPD和△CQP中,
 ,
,
∴△BPD≌△CQP
(3)
解:点P、Q的运动速度不相等时,△BPD与△CQP全等,则CP=BP,
即t= ![]() =
= ![]() 秒,
秒,
∵AB=16,点D为AB的中点,
∴BD=8,
则CQ=8,
∴点Q的运动速度a=8÷ ![]() =
= ![]() ,
,
∴当点Q的运动速度a为 ![]() 厘米/秒时,△BPD与△CQP全等
厘米/秒时,△BPD与△CQP全等
【解析】(1)根据题意、结合图形解答;(2)分别求出BP、CQ的长,根据全等三角形的判定定理解答;(3)根据全等三角形的性质求出△BPD与△CQP全等时CQ的长,根据速度公式计算即可.
-
科目: 来源: 题型:
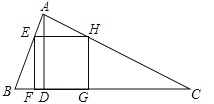
查看答案和解析>>【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设点(﹣1,y1),(2,y2),(3,y3)是抛物线y=﹣x2+a上的三点,则y1、y2、y3的大小关系为( )
A.y3>y2>y1B.y1>y3>y2C.y3>y1>y2D.y1>y2>y3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为2的等边三角形,D是CA延长线上一点,以BD为边长作等边三角形BDE,连接AE.求:
①∠EAD的度数;
②求AE﹣AD的值.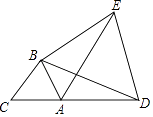
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车队要把4000吨货物运到雅安地震灾区(方案定后,每天的运量不变)。
(1)从运输开始,每天运输的货物吨数n(单位:吨)与运输时间t(单位:天)之间有怎样的函数关系式?
(2)因地震,到灾区的道路受阻,实际每天比原计划少运20%,则推迟1天完成任务,求原计划完成任务的天数. -
科目: 来源: 题型:
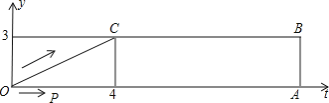
查看答案和解析>>【题目】如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动.设P从出发起运动了t秒.
(1)如果点Q的速度为每秒2个单位,①试分别写出这时点Q在OC上或在CB上时的坐标(用含t的代数式表示,不要求写出t的取值范围);
②求t为何值时,PQ∥OC?
(2)如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半,①试用含t的代数式表示这时点Q所经过的路程和它的速度;
②试问:这时直线PQ是否可能同时把梯形OABC的面积也分成相等的两部分?如有可能,求出相应的t的值和P、Q的坐标;如不可能,请说明理由.
-
科目: 来源: 题型:
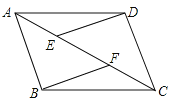
查看答案和解析>>【题目】如图,在ABCD中,E、F为对角线AC上的两点,且AE=CF,连接DE、BF,
(1)写出图中所有的全等三角形;
(2)求证:DE∥BF.
相关试题

