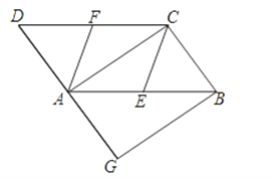
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,AC是对角线,过点B作BG∥AC交DA的延长线于点G.
(1)求证:CE∥AF;
(2)若∠G=90°,求证:四边形CEAF是菱形.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)根据已知条件证明AE=CF,AE∥CF,从而得出四边形DFBE是平行四边形,即可证明CE∥AF;
(2)先证明CE=AE,再根据邻边相等的平行四边形是菱形,从而得出结论.
试题解析:(1)在□ABCD中,AB∥CD,AB=CD,
∵E、F分别为边AB、CD的中点,
∴CF=![]() CD,AE=
CD,AE=![]() AB,
AB,
∴CF∥AE,CF=AE,
∴四边形CEAF为平行四边形,
∴CE∥AF;
(2)∵BG∥AC,
∴∠G=∠DAC=90°,
∴△DAC为直角三角形,
又∵F为边CD的中点,
∴AF=![]() CD=CF,
CD=CF,
又∵四边形CEAF为平行四边形,
∴四边形CEAF为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知M(x﹣2,x+1)在x轴上,则x的值为_____.
-
科目: 来源: 题型:
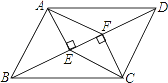
查看答案和解析>>【题目】如图,在ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断四边形AECF是不是平行四边形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,3),B(﹣1,b),且AB⊥x轴,若两点的距离为5,则满足条件的a的值为_____,b的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.
(1)依题意,补全图形;
(2)求证:四边形EFMN是矩形;
(3)连接DM,若DM⊥AC于点M,ON=3,求矩形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB∥CD,∠A = ∠D,试说明 AC∥DE 成立的理由.

下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整。
解:∵ AB ∥ CD (已知)
∴ ∠A = (两直线平行,内错角相等)
又∵ ∠A = ∠D( )
∴ ∠ = ∠ (等量代换)
∴ AC ∥ DE ( )
-
科目: 来源: 题型:
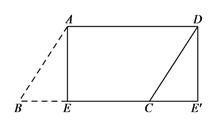
查看答案和解析>>【题目】(1)如图,纸片□ABCD中,AD=5,S□ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为( )
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.
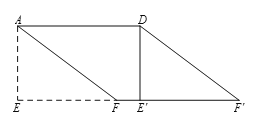
①求证:四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长.
相关试题

