【题目】已知:关于x的一元二次方程mx2-3(m-1)x+2m-3=0(m>3).
(1)求证:方程总有两个不相等的实数根;
(2)设方程的两个实数根分别为x1,x2,且x1<x2.
①求方程的两个实数根x1,x2(用含m的代数式表示);
②若mx1<8-4x2,直接写出m的取值范围.
参考答案:
【答案】(1)证明见解析;(2)①x1=1,x2=![]() ;②
;②![]() .
.
【解析】(1)由于m>3,此方程为关于x的一元二次方程,再计算出判别式△=(m-3)2,然后根据判别式的意义即可得到结论;
(2)②由求根公式得到x=1,或x=![]() ,即可得到结论;②根据mx1<8-4x2,即可得到 结果.
,即可得到结论;②根据mx1<8-4x2,即可得到 结果.
(1)证明:∵mx2-3(m-1)x+2m-3=0(m>3)是关于x的一元二次方程,
∴△=[(-3(m-1)]2-4m(2m-3)=m2-6m+9=(m-3)2,
∵m>3,
∴(m-3)2>0,即△>0,
∴方程总有两个不相等的实数根;
(2)①由求根公式得x=![]() ,
,
∴x=1,或x=![]() ,
,
当x1=1,x2=2-![]() ,
,
②则mx1<8-4x2,
即m<8-8+![]() ,
,
∴3<m<2![]() ;
;
当x1=2-![]() ,x2=1,
,x2=1,
则2m-3<4,
∴3<m<![]() .
.
综上所述,3<m<2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN.连接AN,CN,取AN的中点E,连接BE,AC,交于F点.
(1) ①依题意补全图形;
②求证:BE⊥AC.
(2)请探究线段BE,AD,CN所满足的等量关系,并证明你的结论.
(3)设AB=1,若点M沿着线段CD从点C运动到点D,则在该运动过程中,线段EN所扫过的面积为______________(直接写出答案).

-
科目: 来源: 题型:
查看答案和解析>>【题目】【概念学习】规定:求若干个相同的有理数(均不等于0)的除法运算叫除方,如
 ,
,  等.类比有理数乘方,我们把
等.类比有理数乘方,我们把 记作
记作 ,读作“2的圈3次方”,
,读作“2的圈3次方”,  记作
记作 ,读作“
,读作“ 的圈4次方”.一般地,把
的圈4次方”.一般地,把 (
( ≠0)记作
≠0)记作 ,读作“a的圈c次方”.
,读作“a的圈c次方”.【初步探究】
(1)直接写出计算结果:
 =______________,
=______________,  =______________.
=______________.(2)关于除方,下列说法错误的是( )
A.任何非零数的圈3次方都等于它的倒数 B.对于任何正整数c,
 =1
=1C.
 D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数【深入思考】
我们知道有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?

 =
= =
=

(1)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
 =___________;
=___________;  =_____________;
=_____________;  =____________.
=____________.(2)想一想:将一个非零有理数a的圈c(c≥3)次方写成幂的形式等于___________.
(3)算一算:
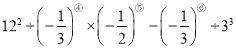
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.

(1)请补全下表:
30°
45°
60°
90°
120°
135°
150°
S

1

(2)填空:
由(1)可以发现正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把菱形的面积S记为S(α).例如:当α=30°时,
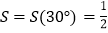 ;当α=135°时,
;当α=135°时,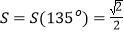 .由上表可以得到
.由上表可以得到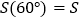 ( ______°);
( ______°);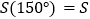 ( ______°),…,由此可以归纳出
( ______°),…,由此可以归纳出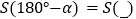 .
.(3) 两块相同的等腰直角三角板按如图的方式放置,AD=
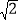 ,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).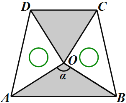
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
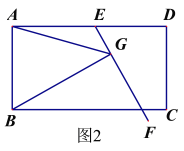
问题:如图1,在平行四边形ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
求证:EG =AG+BG.
小明同学的思路是:作∠GAH=∠EAB交GE于点H,构造全等三角形,经过推理解决问题.
参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EG、AG、BG之间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】AB为⊙O直径,BC为⊙O切线,切点为B,CO平行于弦AD,作直线DC.
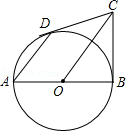
①求证:DC为⊙O切线;
②若ADOC=8,求⊙O半径r. -
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
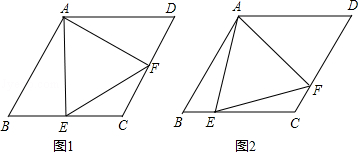
(1)如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图2,若∠EAF=60°,求证:△AEF是等边三角形.
相关试题

