Question

【题目】如图，已知正方形ABCD的边长为1，连接AC、BD，CE平分∠ACD交BD于点E，则DE= ．

Answer 1

【答案】 ﹣1
【解析】解：过E作EF⊥DC于F， ∵四边形ABCD是正方形，
∴AC⊥BD，
∵CE平分∠ACD交BD于点E，
∴EO=EF，
在Rt△COE和Rt△CFE中
，
∴Rt△COE≌Rt△CFE（HL），
∴CO=FC，
∵正方形ABCD的边长为1，
∴AC= ，
∴CO= AC= ，
∴CF=CO= ，
∴EF=DF=DC﹣CF=1﹣ ，
∴DE= = ﹣1，
另法：因为四边形ABCD是正方形，
∴∠ACB=45°=∠DBC=∠DAC，
∵CE平分∠ACD交BD于点E，
∴∠ACE=∠DCE=22.5°，
∴∠BCE=45°+22.5°=67.5°，
∵∠CBE=45°，
∴∠BEC=67.5°，
∴BE=BC，
∵正方形ABCD的边长为1，
∴BC=1，
∴BE=1，
∵正方形ABCD的边长为1，
∴AC= ，
∴DE= ﹣1，
故答案为： ﹣1．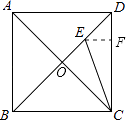

过E作EF⊥DC于F，根据正方形的性质和角平分线的性质以及勾股定理即可求出DE的长．