Question

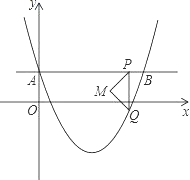
【题目】如图，在平面直角坐标系中，抛物线y=a（x-2）2-2与y轴交于点A（0，1），直线AB∥x轴交抛物线于点B，点P是直线AB上一点（不与A、B重合），PQ∥y轴交抛物线于点Q，以PQ为斜边向左作等腰直角三角形PQM，设点P的横坐标为m．

（1）求这条抛物线所对应的函数表达式．

（2）当线段PQ被x轴平分时，求m的值．

（3）当等腰直角三角形PQM夹在x轴与直线AB之间的图形为轴对称三角形时，求m的取值范围．

（4）直接写出当等腰直角三角形PQM的两条直角边与坐标轴有两个公共点时m的取值范围．

Answer 1

【答案】（1）y=（x-2）2-2，（2）m1=2+，m2=2-．（3）0＜m≤2-或2-≤m≤2+或2+≤m＜4，（4）0＜m＜或m＞．

【解析】

试题分析：（1）将A点坐标代入解析式直接求出a；

（2）由P、Q关于x轴对称，且横坐标相同可设出Q点坐标，代入抛物线解析式中，即可直接求出m的值；

（3）找到两个临界点：当Q点刚好在x轴上时；当M点刚好在x轴上时．算出这个两个临界状态时的m值，即可确定符合要求的m的取值范围；

（4）等腰直角三角形PQM的两条直角边与坐标轴有两个公共点，也就是y轴同时与两直角边相交，所以只需算出M点恰好在y轴上的临界状态时的m值即可．

试题解析：（1）把A（0，1）代入y=a（x-2）2-2中，得1=a（0-2）2-2，

∴a=，

∴y=（x-2）2-2，

（2）设Q（m，-1），

则-1=（m-2）2-2，

∴m1=2+，m2=2-．

（3）当点Q落在x轴上时，PQ=1，

∴1-[（m-2）2-2]=1，

∴m1=2-，m2=2+，

∴当0＜m≤2-或2-≤m≤2+或2+≤m＜4，为轴对称三角形，

（4）当M点刚好在y轴上时：|1-[（m-2）2-2]|=m，

解得：m=或m=，

∴0＜m＜或m＞．