【题目】在□ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连接EG、GF、FH、HE.
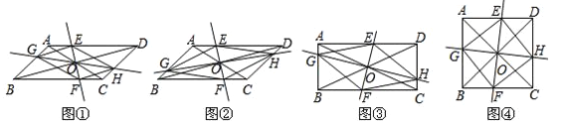
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
参考答案:
【答案】(1)四边形EGFH是平行四边形;(2)菱形;(3)菱形;(4)四边形EGFH是正方形.
【解析】
试题分析:(1)由于平行四边形对角线的交点是它的对称中心,即可得出OE=OF、OG=OH;根据对角线互相平分的四边形是平行四边形即可判断出EGFH的性质;
(2)当EF⊥GH时,平行四边形EGFH的对角线互相垂直平分,故四边形EGFH是菱形;
(3)当AC=BD时,对四边形EGFH的形状不会产生影响,故结论同(2);
(4)当AC=BD且AC⊥BD时,四边形ABCD是正方形,则对角线相等且互相垂直平分;可通过证△BOG≌△COF,得OG=OF,从而证得菱形的对角线相等,根据对角线相等的菱形是正方形即可判断出EGFH的形状.
试题解析:(1)四边形EGFH是平行四边形;
证明:∵ABCD的对角线AC、BD交于点O
∴点O是ABCD的对称中心;
∴EO=FO,GO=HO;
∴四边形EGFH是平行四边形;
(2)∵四边形EGFH是平行四边形,EF⊥GH,
∴四边形EGFH是菱形;
(3)菱形;
由(2)知四边形EGFH是菱形,
当AC=BD时,对四边形EGFH的形状不会产生影响;
(4)四边形EGFH是正方形;
证明:∵AC=BD,
∴ABCD是矩形;
又∵AC⊥BD,
∴ABCD是正方形,
∴∠BOC=90°,∠GBO=∠FCO=45°,OB=OC;
∵EF⊥GH,
∴∠GOF=90°;
∠BOG+∠BOF=∠COF+∠BOF=90°
∴∠BOG=∠COF;
∴△BOG≌△COF(ASA);
∴OG=OF,同理可得:EO=OH,
∴GH=EF;
由(3)知四边形EGFH是菱形,
又EF=GH,
∴四边形EGFH是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;(2)求BG的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列不等式变形正确的是( )
A.若a>b,则a﹣2>b﹣2
B.若- ?a<2,则a<﹣4
?a<2,则a<﹣4
C.若a>b,则1﹣2a>1﹣2b
D.若a<b,则ac2<bc2 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲布袋中有三个红球,分别标有数字1,2,3;乙布袋中有三个白球,分别标有数字2,3,4.这些球除颜色和数字外完全相同.小亮从甲袋中随机摸出一个红球,小刚从乙袋中随机摸出一个白球.
(1)用画树状图(树形图)或列表的方法,求摸出的两个球上的数字之和为6的概率;
(2)小亮和小刚做游戏,规则是:若摸出的两个球上的数字之和为奇数,小亮胜;否则,小刚胜.你认为这个游戏公平吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017的相反数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(﹣1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )
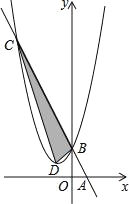
A.8:1 B.6:1 C.5:1 D.4:1
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.在同一年出生的400人中至少有两人的生日相同
B.投掷一粒骰子,连投两次点数相同的概率与连投两次点数都为1的概率是相等的
C.从一副完整的扑克牌中随机抽取一张牌恰好是红桃K,这是必然事件
D.一个袋中装有3个红球,5个白球,任意摸出一个球是红球的概率是
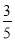
相关试题

