【题目】如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )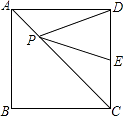
A.3 ![]()
B.10 ![]()
C.9
D.9 ![]()
参考答案:
【答案】A
【解析】如图,连接BE,设BE与AC交于点P′,
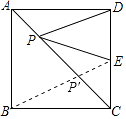
∵四边形ABCD是正方形,
∴点B与D关于AC对称,
∴P′D=P′B,
∴P′D+P′E=P′B+P′E=BE最小.
即P在AC与BE的交点上时,PD+PE最小,为BE的长度.
∵直角△CBE中,∠BCE=90°,BC=9,CE= ![]() CD=3,
CD=3,
∴BE= ![]() =3
=3 ![]() .
.
所以答案是:A.
【考点精析】认真审题,首先需要了解正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形),还要掌握轴对称的性质(关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.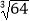 =8
=8
B.(x+3)2=x2+9
C.(ab3)2=ab6
D.(π﹣3.14)0=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各个选项中的网格都是边长为1的小正方形,利用函数的图象解方程
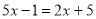 ,其中正确的是( )
,其中正确的是( )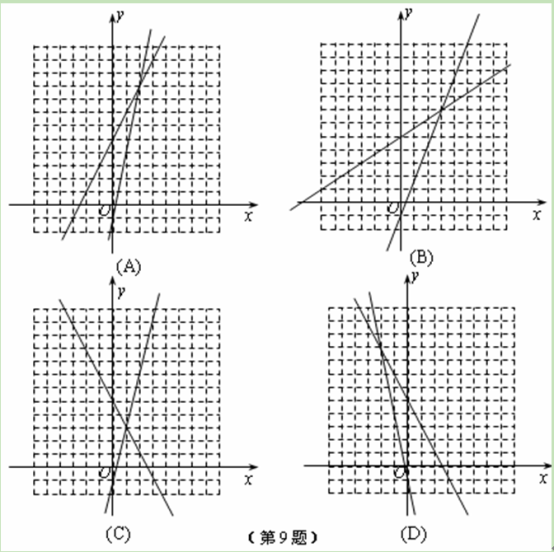
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,建筑工人砌墙时,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的参照线,其运用到的数学原理是( )

A.两点之间,线段最短
B.两点确定一条直线
C.垂线段最短
D.过一点有且只有一条直线和已知直线平行 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG//BC,且
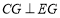 于G,下列结论:①
于G,下列结论:①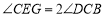 ;②
;②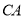 平分
平分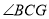 ;③
;③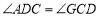 ;④
;④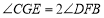 ;其中正确的结论是( )
;其中正确的结论是( )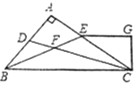
A.只有①③B.只有①③④C.只有②④D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(
 ,﹣2);⑤当x<
,﹣2);⑤当x<  时,y随x的增大而减小;⑥a+b+c>0正确的有( )
时,y随x的增大而减小;⑥a+b+c>0正确的有( )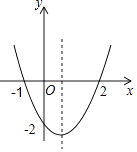
A.3个
B.4个
C.5个
D.6个 -
科目: 来源: 题型:
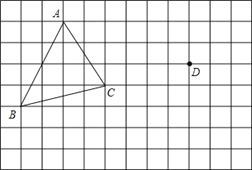
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF,并求△DEF的面积=
(2)若连接AD、CF,则这两条线段之间的关系是_________________;
(3)请在AB上找一点P,使得线段CP平分△ABC的面积,在图上作出线段CP.
相关试题

