【题目】如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF.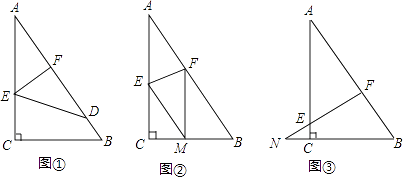
(1)图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF , 求AE的长;
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图③,若FE的延长线与BC的延长线交于点N,CN=1,CE= ![]() ,求
,求 ![]() 的值.
的值.
参考答案:
【答案】
(1)
解:如图①,

∵△ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,
∴EF⊥AB,△AEF≌△DEF,
∴S△AEF≌S△DEF,
∵S四边形ECBF=3S△EDF,
∴S△ABC=4S△AEF,
在Rt△ABC中,∵∠ACB=90°,AC=4,BC=3,
∴AB= ![]() =5,
=5,
∵∠EAF=∠BAC,
∴Rt△AEF∽Rt△ABC,
∴ ![]() =(
=( ![]() )2,即(
)2,即( ![]() )2=
)2= ![]() ,
,
∴AE= ![]() ;
;
(2)
解:①四边形AEMF为菱形.理由如下:
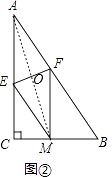
如图②,∵△ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,
∴AE=EM,AF=MF,∠AFE=∠MFE,
∵MF∥AC,
∴∠AEF=∠MFE,
∴∠AEF=∠AFE,
∴AE=AF,
∴AE=EM=MF=AF,
∴四边形AEMF为菱形;
②连结AM交EF于点O,如图②,
设AE=x,则EM=x,CE=4﹣x,
∵四边形AEMF为菱形,
∴EM∥AB,
∴△CME∽△CBA,
∴ ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,解得x=
,解得x= ![]() ,CM=
,CM= ![]() ,
,
在Rt△ACM中,AM= ![]() =
= ![]() =
= ![]() ,
,
∵S菱形AEMF= ![]() EFAM=AECM,
EFAM=AECM,
∴EF=2× ![]() =
= ![]() ;
;
(3)
解:如图③,
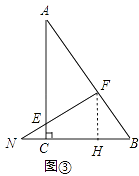
作FH⊥BC于H,
∵EC∥FH,
∴△NCE∽△NFH,
∴CN:NH=CE:FH,即1:NH= ![]() :FH,
:FH,
∴FH:NH=4:7,
设FH=4x,NH=7x,则CH=7x﹣1,BH=3﹣(7x﹣1)=4﹣7x,
∵FH∥AC,
∴△BFH∽△BAC,
∴BH:BC=FH:AC,即(4﹣7x):3=4x:4,解得x= ![]() ,
,
∴FH=4x= ![]() ,BH=4﹣7x=
,BH=4﹣7x= ![]() ,
,
在Rt△BFH中,BF= ![]() =2,
=2,
∴AF=AB﹣BF=5﹣2=3,
∴ ![]() =
= ![]() .
.
【解析】本题考查了三角形的综合题:熟练掌握折叠的性质和菱形的判定与性质;灵活构建相似三角形,运用勾股定理或相似比表示线段之间的关系和计算线段的长.解决此类题目时要各个击破.(1)先利用折叠的性质得到EF⊥AB,△AEF≌△DEF,则S△AEF≌S△DEF , 则易得S△ABC=4S△AEF , 再证明Rt△AEF∽Rt△ABC,然后根据相似三角形的性质得到 ![]() =(
=( ![]() )2 , 再利用勾股定理求出AB即可得到AE的长;(2)①通过证明四条边相等判断四边形AEMF为菱形;②连结AM交EF于点O,如图②,设AE=x,则EM=x,CE=4﹣x,先证明△CME∽△CBA得到
)2 , 再利用勾股定理求出AB即可得到AE的长;(2)①通过证明四条边相等判断四边形AEMF为菱形;②连结AM交EF于点O,如图②,设AE=x,则EM=x,CE=4﹣x,先证明△CME∽△CBA得到 ![]() =
= ![]() =
= ![]() ,解出x后计算出CM=
,解出x后计算出CM= ![]() ,再利用勾股定理计算出AM,然后根据菱形的面积公式计算EF;(3)如图③,作FH⊥BC于H,先证明△NCE∽△NFH,利用相似比得到FH:NH=4:7,设FH=4x,NH=7x,则CH=7x﹣1,BH=3﹣(7x﹣1)=4﹣7x,再证明△BFH∽△BAC,利用相似比可计算出x=
,再利用勾股定理计算出AM,然后根据菱形的面积公式计算EF;(3)如图③,作FH⊥BC于H,先证明△NCE∽△NFH,利用相似比得到FH:NH=4:7,设FH=4x,NH=7x,则CH=7x﹣1,BH=3﹣(7x﹣1)=4﹣7x,再证明△BFH∽△BAC,利用相似比可计算出x= ![]() ,则可计算出FH和BH,接着利用勾股定理计算出BF,从而得到AF的长,于是可计算出
,则可计算出FH和BH,接着利用勾股定理计算出BF,从而得到AF的长,于是可计算出 ![]() 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天)
1
30
60
90
每天销售量p(件)
198
140
80
20

(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在菱形ABCD中,AC=2,BD=2
 ,AC,BD相交于点O.
,AC,BD相交于点O. 
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G. ①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线y=
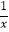 (x>0),直线l1:y﹣
(x>0),直线l1:y﹣ 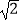 =k(x﹣
=k(x﹣ 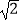 )(k<0)过定点F且与双曲线交于A,B两点,设A(x1 , y1),B(x2 , y2)(x1<x2),直线l2:y=﹣x+
)(k<0)过定点F且与双曲线交于A,B两点,设A(x1 , y1),B(x2 , y2)(x1<x2),直线l2:y=﹣x+ 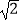 .
.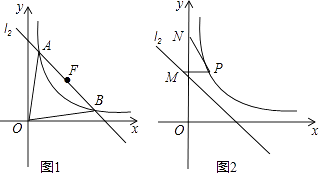
(1)若k=﹣1,求△OAB的面积S;
(2)若AB=
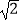 ,求k的值;
,求k的值;
(3)设N(0,2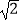 ),P在双曲线上,M在直线l2上且PM∥x轴,问在第二象限内是否存在一点Q,使得四边形QMPN是周长最小的平行四边形?若存在,请求出Q点的坐标.
),P在双曲线上,M在直线l2上且PM∥x轴,问在第二象限内是否存在一点Q,使得四边形QMPN是周长最小的平行四边形?若存在,请求出Q点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
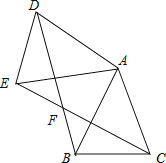
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.

(1)求证:AC2=CDBC;
(2)过E作EG⊥AB,并延长EG至点K,使EK=EB.
①若点H是点D关于AC的对称点,点F为AC的中点,求证:FH⊥GH;
②若∠B=30°,求证:四边形AKEC是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,AB≠CD,BD=AC.

(1)求证:AD=BC;
(2)若E、F、G、H分别是AB、CD、AC、BD的中点,求证:线段EF与线段GH互相垂直平分.
相关试题

