【题目】如图,半径为1个单位的圆片上有一点Q与数轴上的原点重合(提示:圆的周长C=2πr)
(1)把圆片沿数轴向左滚动1周,点Q到达数轴上点A的位置,点A表示的数是;
(2)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:
+2,﹣1,﹣5,+4,+3,﹣2
①第几次滚动后,Q点距离原点最近?第几次滚动后,Q点距离原点最远?
②当圆片结束运动时,Q点运动的路程共有多少?此时点Q所表示的数是多少?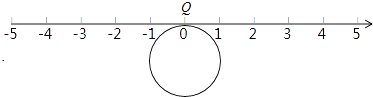
参考答案:
【答案】
(1)﹣2π
(2)解:①第4次滚动后Q点离原点最近,第3次滚动后,Q点离原点最远;
②|﹢2|+|﹣1|+|﹣5|+|+4|+|+3|+|﹣2|=17,
Q点运动的路程共有:17×2π×1=34π;
(+2)+(﹣1)+(﹣5)+(+4 )+(+3 )+(﹣2)=1,
1×2π=2π,此时点Q所表示的数是2π
【解析】解:(1)把圆片沿数轴向左滚动1周,点Q到达数轴上点A的位置,点A表示的数是﹣2π;故答案为:﹣2π;
(1)利用圆的半径以及滚动周数即可得出滚动距离;(2)①利用滚动的方向以及滚动的周数即可得出Q点移动距离变化;②利用绝对值得性质以及有理数的加减运算得出移动距离和Q表示的数即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 数据3,4,4,7,3的众数是4
B. 数据0,1,2,5,a的中位数是2
C. 一组数据的众数和中位数不可能相等
D. 数据0,5,-7,-5,7的中位数和平均数都是0
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图10×9的网格图中,△ABC和△CDE都是等腰直角三角,其顶点都在格点上,若点A、C的坐标分别为(﹣5,﹣2)和(﹣1,0).
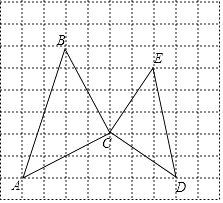
(1)建立平面直角坐标系,写出点B、D、E的坐标;
(2)求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】若m-n=-1,则(m-n)-2(m-n)的值是( )
A. 3 B. 2 C. 1 D. -1
-
科目: 来源: 题型:
查看答案和解析>>【题目】人写字时眼睛和笔端的距离超过30cm时则符合保护视力的要求.图1是一位同学的坐姿,把她的眼睛B、肘关节C和笔端A的位置关系抽象成图2的△ABC,BC=30cm,AC=22cm,∠ACB=530,她的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin530≈0.8,cos530≈0.6,tan530≈1.3)

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情景:
如图,在直角坐标系xOy中,点A、B为二次函数y=ax2(a>0)图象上的两点,且点A、B的横坐标分别为m、n(m>n>0),连接OA、AB、OB.设△AOB的面积为S时,解答下列问题:
探究:当a=1时,
mn
m
 n
nS
m=3,n=1
3
2
m=5,n=2
10
3
当a=2时,
2mn
m
 n
nS
m=3,n=1
6
2
m=5,n=2
20
3
归纳证明:
对任意m、n(m>n>0),猜想S=_________________ (用a,m,n表示),并证明你的猜想.
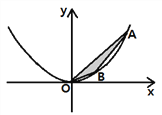
拓展应用:
若点A、B的横坐标分别为m、n(m>0>n),其它条件不变时,△AOB的面积S=____ (用a, m,n表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】【知识背景】在学习计算框图时,可以用“
 ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“  ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“  ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条) 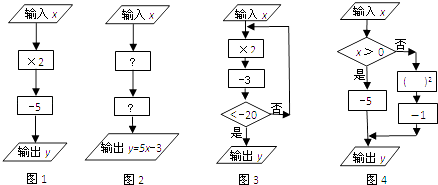
【尝试解决】
(1)①如图1,当输入数x=﹣2时,输出数y=;
②如图2,第一个“ ”内,应填; 第二个“
”内,应填; 第二个“  ”内,应填;
”内,应填;
(2)①如图3,当输入数x=﹣1时,输出数y=;②如图4,当输出的值y=17,则输入的值x=;
(3)为鼓励节约用水,决定对用水实行“阶梯价”:当每月用水量不超过10吨时(含10吨),以3元/吨的价格收费;当每月用水量超过10吨时,超过部分以4元/吨的价格收费.请设计出一个“计算框图”,使得输入数为用水量x,输出数为水费y.
相关试题

