【题目】如图,四边形OABC为直角梯形,已知AB∥OC,BC⊥OC,A点坐标为(3,4),AB=6.
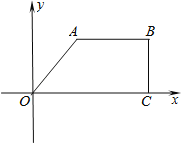
(1)求出直线OA的函数解析式;
(2)求出梯形OABC的周长;
(3)若直线l经过点D(3,0),且直线l将直角梯形OABC的面积分成相等的两部分,试求出直线l的函数解析式.
(4)若直线l经过点D(3,0),且直线l将直角梯形OABC的周长分为5:7两部分,试求出直线l的函数解析式.
参考答案:
【答案】(1)y=![]() x.(2)24.(3)y=
x.(2)24.(3)y=![]() x﹣8.(4)y=
x﹣8.(4)y=![]() x﹣2.
x﹣2.
【解析】解:(1)设OA的解析式为y=kx,
则3k=4,
∴k=![]() .
.
∴OA的解析式为y=![]() x.
x.
(2)如图,延长BA交y轴于点D.
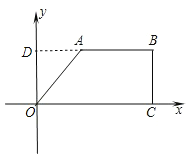
∵BA∥OC,
∴AD⊥y轴.且AD=3,OD=4.
∴AO=5,∴DB=3+6=9.
∴OC=9,又BC=OD=4.
∴COABC=OA+AB+BC+OC=5+6+4+9=24.
(3)如图
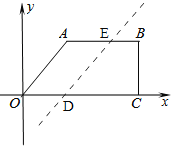
设点E的坐标为(a,4),
∴AE=a﹣3,
由(2)得AB=6,OC=9,BC=4,
∴S梯形OABC=![]() (AB+OC)×BC=
(AB+OC)×BC=![]() (6+9)×4=30,
(6+9)×4=30,
∵直线l经过点D(3,0),
∴OD=3,
∵直线l将直角梯形OABC的面积分成相等的两部分,
∴S梯形OAED=![]() S梯形OABC=
S梯形OABC=![]() ×30=15,
×30=15,
∴S梯形OAED=![]() (AE+OD)×BC=
(AE+OD)×BC=![]() ×(a﹣3+3)×4=15,
×(a﹣3+3)×4=15,
∴a=![]() ,
,
∴E(![]() ,4),
,4),
∵D(3,0),
∴直线解析式为y=![]() x﹣8.
x﹣8.
(4)∵COABC=24,故被l分成的两部分分别为10和14.
若l左边部分为10,则s=10﹣3=7,
∴P(5,4).
设PD为:y=mx+n,则![]() ,
,
∴![]() ,
,
∴y=2x﹣6;
若l左边部分为14,则s=14﹣3=11,
∴P(9,4).
∴![]() ,
,
∴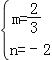 ,
,
∴y=![]() x﹣2.
x﹣2.
-
科目: 来源: 题型:
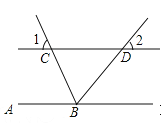
查看答案和解析>>【题目】如图,直线AB∥CD,BC平分∠ABD,若∠1=54°,则∠2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.
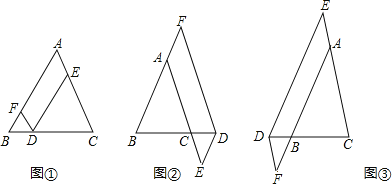
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
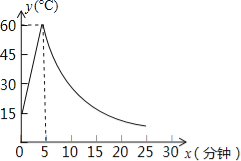
(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:x2(x﹣1)﹣x(x2+x﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列从左边到右边的变形,是因式分解的是( )
A. y2﹣2y+4=(y﹣2)2
B. 10x2﹣5x=5x(2x﹣1)
C. a(x+y)=ax+ay
D. t2﹣16+3t=(t+4)(t﹣4)+3t
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2=4x的解 .
相关试题

