【题目】如图,在ABCD中,∠ADB=90°,点E为AB边的中点,点F为CD边的中点. 
(1)求证:四边形DEBF是菱形;
(2)若∠A=45°,求证:四边形DEBF是正方形.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB,
∵点E为AB边的中点,点F为CD边的中点,
∴DF∥BE,DF=BE,
∴四边形DEBF是平行四边形,
∵∠ADB=90°,点E为AB边的中点,
∴DE=BE=AE,
∴四边形DEBF是菱形;
(2)解:∵∠ADB=90°,∠A=45°,
∴∠A=∠ABD=45°,
∴AD=BD,
∵E为AB的中点,
∴DE⊥AB,
即∠DEB=90°,
∵四边形DEBF是菱形,
∴四边形DEBF是正方形.
【解析】(1)根据平行四边形的性质得出DC∥AB,DC=AB,求出DF∥BE,DF=BE,得出四边形DEBF是平行四边形,求出DE=BE,根据菱形的判定得出即可;(2)求出AD=BD,根据等腰三角形的性质得出DE⊥AB,根据正方形的判定得出即可.
【考点精析】根据题目的已知条件,利用直角三角形斜边上的中线和平行四边形的性质的相关知识可以得到问题的答案,需要掌握直角三角形斜边上的中线等于斜边的一半;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】能说明命题“若a>b,则ac>bc”是假命题的一个c值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=
 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.(1)求函数y=kx+b和y=
 的表达式;
的表达式;(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆是一座美丽的山坡,某中学依山而建,校门A处,有一斜坡AB,长度为13米,在坡顶B处看教学楼CF的楼顶C的仰角∠CBF=53°,离B点4米远的E处有一花台,在E处仰望C的仰角∠CEF=63.4°,CF的延长线交校门处的水平面于D点,FD=5米.
(1)求斜坡AB的坡度i;(2)求DC的长.(参考数据:tan53°≈
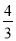 ,tan63.4°≈2)
,tan63.4°≈2)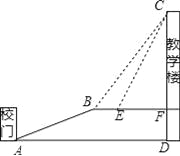
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生会向全校1900名学生发起了爱心捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答系列问题:

(1)本次接受随机抽样调查的学生人数为人,图1中m的值是 .
(2)求本次调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】光明科学城规划总面积达99000000平方米,将对标全球最高标准、最好水平.其中99000000用科学记数法表示为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从M、N两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图是甲乙两车之间的距离s(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达N地,停止行驶.

(1)甲车的速度是千米/小时;乙车速度是千米/小时;a= .
(2)甲车出发多长时间后两车相距330千米?
相关试题

