【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.

参考答案:
【答案】(1)y=2x﹣5,y=![]() ;(2)(2.5,0).
;(2)(2.5,0).
【解析】(1)利用待定系数法即可解答;
(2)设点M的坐标为(x,2x﹣5),根据MB=MC,得到![]() ,即可解答.
,即可解答.
(1)把点A(4,3)代入函数y=![]() 得:a=3×4=12,∴y=
得:a=3×4=12,∴y=![]() .OA=
.OA=![]() =5,
=5,
∵OA=OB,∴OB=5,∴点B的坐标为(0,﹣5),
把B(0,﹣5),A(4,3)代入y=kx+b得:![]() 解得:
解得:![]() ∴y=2x﹣5.
∴y=2x﹣5.
(2)∵点M在一次函数y=2x﹣5上,∴设点M的坐标为(x,2x﹣5),
∵MB=MC,∴![]()
解得:x=2.5,∴点M的坐标为(2.5,0).
“点睛”本题考查了一次函数与反比例函数的交点,解决本题的关键是利用待定系数法求解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AC=3,BC=2,则线段AB的长度( )
A. 一定是5 B. 一定是1 C. 一定是5或1 D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程3x-7(x-1)=-2(x+3)+3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】3xmy4与x3yn是同类项,则2m-n=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲同学手中藏有三张分别标有数字
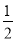 、
、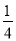 、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.(1)请你用树形图或列表法列出所有可能的结果;
(2)现制定一个游戏规则:若所选出的a,b能使得ax2+bx+1=0有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请用概率知识解释.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE,点M、N分别是BD、GE的中点,若BC=14,CE=2,则MN的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB∥DF,∠D+∠B=180°,
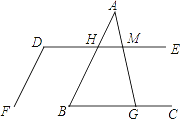
(1)求证:DE∥BC;
(2)如果∠AMD=75°,求∠AGC的度数.
相关试题

