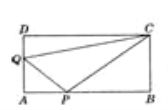
【题目】如图,在矩形AB CD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动;点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0<t<6).
(1)当t为何值时,△QAP为等腰直角三角形?
(2)四边形QAPC的面积与t的大小有关系吗?请说明理由.
参考答案:
【答案】(1)t为2秒时,△QAP为等腰直角三角形;
(2)四边形QAPC的面积与t的大小没有关系
【解析】试题分析:(1)根据题意得到AP=2t,DQ=t,根据等腰直角三角形的性质列出方程,解方程即可;(2)根据四边形QAPC的面积=四边形ABCD的面积-△CDQ的面积-△PBC的面积计算;
试题解析:
(1)∵当QA=AP时,△QAP为等腰直角三角形.
∴![]() 解得:
解得: ![]() ,
,
即t为2秒时,△QAP为等腰直角三角形.
(2)四边形QAPC的面积=![]() 为常数.
为常数.
所以四边形QAPC的面积与t的大小没有关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种植物的主干长出若干数目的支干,每个支干又长出相同数目的小分支,若小分支、支干和主干的总数目是73,则每个支干长出的小分支的数目为( )
A. 7 B. 8 C. 9 D. 10
-
科目: 来源: 题型:
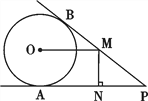
查看答案和解析>>【题目】如图,PA,PB分别与⊙O相切于点A,B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
(1)求证:OM = AN;
(2)若⊙O的半径R = 3,PA = 9,求OM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品价格为33元/件,某人只带有2元和5元的两种面值的购物劵各若干张,买了一件这种商品;若无需找零钱,则付款方式中张数之和(指付2元和5元购物券的张数)最少和张数之和最多的方式分别是( )
A. 8张和16张 B. 8张和15张 C. 9张和16张 D. 9张和15张
-
科目: 来源: 题型:
查看答案和解析>>【题目】八月份利川市政府计划在总费用2300元的限额内,租用汽车送234名运动员和6名教练到恩施州参加第二届全州青少年运动会,每辆汽车上至少要有1名教练.现有甲、乙两种大客车,它们的载客量和租金如下表:

(1)共需租多少辆汽车?
(2)有几种租车方案?
(3)最节省费用的是哪种租车方案?
-
科目: 来源: 题型:
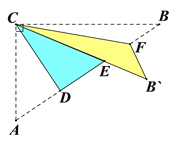
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CD翻折,使点A落在AB上的点E处;再将边BC沿CF翻折,使点B落在CE的延长线上的点B′处,两条折痕与斜边AB分别交于点D、F,则线段B′F的长为( )
A.
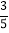 B.
B. 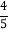 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(﹣3)2的底数是__________,指数是_______________.
相关试题

