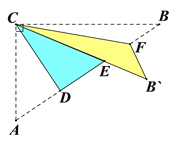
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CD翻折,使点A落在AB上的点E处;再将边BC沿CF翻折,使点B落在CE的延长线上的点B′处,两条折痕与斜边AB分别交于点D、F,则线段B′F的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】B
【解析】首先根据折叠可得CD=AC=3,BC=4,∠ACE=∠DCE,∠BCF=∠B/CF,CE⊥AB,然后求得△BCF是等腰直角三角形,进而求得∠B/GD=90°,CE-EF=![]() ,ED=AE=
,ED=AE=![]() ,
,
从而求得B/D=1,DF=![]() ,在Rt△B/DF中,由勾股定理即可求得B/F的长.
,在Rt△B/DF中,由勾股定理即可求得B/F的长.
解:根据首先根据折叠可得CD=AC=3,B/C=B4,∠ACE=∠DCE,∠BCF=∠B/CF,CE⊥AB,
∴BD=4-3=1,∠DCE+∠B/CF=∠ACE+∠BCF,
∴∠ACB=90°,∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B/FC=135°,
∴∠B/FD=90°,
∵S△ABC=![]() AC×BC=
AC×BC=![]() AB×CE,
AB×CE,
∴AC×BC=AB×CE,
∵根据勾股定理求得AB=5,
∴CE=![]() ,∴EF=
,∴EF=![]() ,ED=AE=
,ED=AE=![]() =
=![]()
∴DE=EF-ED=![]() ,
,
∴B/F=![]() =
=![]() .
.
故答案为:![]()
“点睛”此题主要考查了翻折变换,等腰三角形的判定和性质,勾股定理的应用等,根据折叠的性质求得相等的角是解本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品价格为33元/件,某人只带有2元和5元的两种面值的购物劵各若干张,买了一件这种商品;若无需找零钱,则付款方式中张数之和(指付2元和5元购物券的张数)最少和张数之和最多的方式分别是( )
A. 8张和16张 B. 8张和15张 C. 9张和16张 D. 9张和15张
-
科目: 来源: 题型:
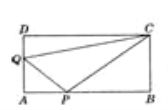
查看答案和解析>>【题目】如图,在矩形AB CD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动;点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0<t<6).
(1)当t为何值时,△QAP为等腰直角三角形?
(2)四边形QAPC的面积与t的大小有关系吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】八月份利川市政府计划在总费用2300元的限额内,租用汽车送234名运动员和6名教练到恩施州参加第二届全州青少年运动会,每辆汽车上至少要有1名教练.现有甲、乙两种大客车,它们的载客量和租金如下表:

(1)共需租多少辆汽车?
(2)有几种租车方案?
(3)最节省费用的是哪种租车方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(﹣3)2的底数是__________,指数是_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2-x-1=0,则代数式-x3+2x2+2 018的值为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市“新媒体”课堂比赛中,7位评委给某位选手的评分不完全相同,若去掉一个最高分,去掉一个最低分,则以下四个统计量中一定不会发生变化的是( )
A. 平均分B. 众数C. 中位数D. 极差
相关试题

