练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在纸板中，，，，是上一点，过点沿直线剪下一个与相似的小三角形纸板，如果有种不同的剪法，那么长的取值范围是________．

    【答案】

    【解析】

    分四种情况讨论，依据相似三角形的对应边成比例，即可得到AP的长的取值范围．

    如图所示，过P作PD∥AB交BC于D或PE∥BC交AB于E，则△PCD∽△ACB或△APE∽△ACB，

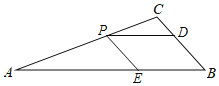
    此时0＜AP＜4；

    如图所示，过P作∠APF=∠B交AB于F，则△APF∽△ABC，

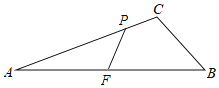
    此时0＜AP≤4；

    如图所示，过P作∠CPG=∠CBA交BC于G，则△CPG∽△CBA，

    此时，△CPG∽△CBA，

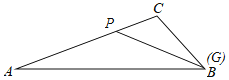
    当点G与点B重合时，CB2=CP×CA，即22=CP×4，

    ∴CP=1，AP=3，

    ∴此时，3≤AP＜4；

    综上所述，AP长的取值范围是3≤AP＜4．

    故答案为：3≤AP＜4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知是的二次函数．

    当取何值时，该二次函数的图象开口向下？

    在的条件下

    ①当取何值时，？？

    ②当时，求的取值范围；

    ③当一时，求的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，D是边AB上一点，E是边AC的中点，作CF∥AB交DE的延长线于点F．

    （1）证明：△ADE≌△CFE；

    （2）若∠B＝∠ACB，CE＝5，CF＝7，求DB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为（a，0），点C的坐标为（0，b），且a、b满足＋|b－6|＝0，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O－C－B－A－O的线路移动．

    （1）a＝______________，b＝_____________，点B的坐标为_______________；

    （2）当点P移动4秒时，请指出点P的位置，并求出点P的坐标；

    （3）在移动过程中，当点P到x轴的距离为5个单位长度时，求点P移动的时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，BE平分∠ABC交AC于点E，过点E作EF∥BC交AB于点F，D是BC边上的中点，连结AD．

    （1）若∠BAD＝55°，求∠C的度数；

    （2）猜想FB与FE的数量关系，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，折叠长方形的一边AD，使点D落在BC边上的点F处，BC＝10，AB＝8

    求．（1）FC的长

    （2）EC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在，的矩形花坛四周修筑小路．

    如图，如果四周的小路的宽均相等，那么小路四周所围成的矩形和矩形相似吗？请说明理由．

    如图，如果相对着的两条小路的宽均相等，试问小路的宽与的比值为多少时，能使小路四周所围成的矩形和矩形相似？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，O为正方形ABCD对角线的交点，E为AB边上一点，F为BC边上一点，△EBF的周长等于BC的长．

    （1）若AB=12，BE=3，求EF的长；

    （2）求∠EOF的度数；

    （3）若OE=OF，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等腰三角形的底边长为，面积是，腰的垂直平分线分别交，于点、，若点为底边的中点，点为线段上一动点，则的周长的最小值为_______.

    查看答案和解析>>

    同步练习册答案