【题目】如图,过点A(﹣1,0)、B(3,0)的抛物线y=﹣x2+bx+c与y轴交于点C,它的对称轴与x轴交于点E.
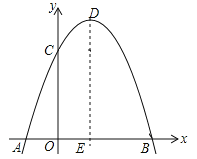
(1)求抛物线解析式;
(2)求抛物线顶点D的坐标;
(3)若抛物线的对称轴上存在点P使S△PCB=3S△POC,求此时DP的长.
参考答案:
【答案】(1)抛物线解析式为y=﹣x2+2x+3;
(2)顶点D的坐标为(1,4);
(3)DP的长为1或5.
【解析】
试题分析:(1)利用待定系数法即可求得解析式;
(2)把抛物线解析式化成顶点式,即可得出顶点坐标;
(3)求出△POC的面积,由三角形的面积关系得出PF=3,求出直线BC的解析式,得出F的坐标,再分两种情况讨论,即可得出DP的长.
试题解析:(1)将A(﹣1,0),B(3,0)代入y=﹣x2+bx+c得:![]() ,
,
解得:b=2,c=3,∴抛物线解析式为y=﹣x2+2x+3;
(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点D的坐标为(1,4);
(3)设BC与抛物线的对称轴交于点F,如图所示:

则点F的横坐标为1,
∵y=﹣x2+2x+3,
当x=0时,y=3,∴OC=3,∴△POC的面积=![]() ×3×1=
×3×1=![]() ,
,
∵△PCB的面积=△PCF的面积+△PBF的面积=![]() PF(1+2)=3×
PF(1+2)=3×![]() ,解得:PF=3,
,解得:PF=3,
设直线BC的解析式为y=kx+a,则![]() ,解得:a=3,k=﹣1,∴直线BC的解析式为y=﹣x+3,
,解得:a=3,k=﹣1,∴直线BC的解析式为y=﹣x+3,
当x=1时,y=2,
∴F的坐标为(1,2),∴EF=2,
当点P在F的上方时,PE=PF+EF=5,∴DP=5﹣4=1;
当点P在F的下方时,PE=PF﹣EF=3﹣2=1,∴DP=4+1=5;
综上所述:DP的长为1或5.
-
科目: 来源: 题型:
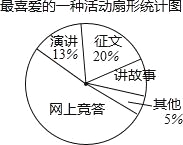
查看答案和解析>>【题目】近期,我市中小学广泛开展了“传承中华文化,共筑精神家园”爱国主义读书教育活动,某中学为了解学生最喜爱的活动形式,以“我最喜爱的一种活动”为主题,进行随机抽样调查,收集数据整理后,绘制出以下两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
最喜爱的一种活动统计表
活动形式
征文
讲故事
演讲
网上竞答
其他
人数
60
30
39
a
b
(1)在这次抽样调查中,一共调查了多少名学生?扇形统计图中“讲故事”部分的圆心角是多少度?
(2)如果这所中学共有学生3800名,那么请你估计最喜爱征文活动的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据9,2,3,一3,1的极差是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是□ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需增加的一个条件是____________

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2+2x﹣3的图象与y轴的交点坐标是( )
A.(0,﹣3)
B.(﹣3,0)
C.(1,0)
D.(0,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如果x<0,y>0,且|x|=2,|y|=3,那么x+y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中装有大小、质地完全相同的4只小球,小球上分别标有1、2、3、4四个数字.
(1)从袋中随机摸出一只小球,求小球上所标数字为奇数的概率;
(2)从袋中随机摸出一只小球,再从剩下的小球中随机摸出一只小球,求两次摸出的小球上所标数字之和为5的概率.
相关试题

