【题目】在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于D;
(1)如果点F与点A重合,且∠C=50°,∠B=30°,如图1,求∠EFD的度数;
(2)如果点F在线段AE上(不与点A重合),如图2,问∠EFD与∠C﹣∠B有怎样的数量关系?并说明理由.
(3)如果点F在△ABC外部,如图3,此时∠EFD与∠C﹣∠B的数量关系是否会发生变化?请说明理由.
参考答案:
【答案】解:(1)∵∠C=50°,∠B=30°,
∴∠BAC=180°﹣50°﹣30°=100°.
∵AE平分∠BAC,
∴∠CAE=50°.
在△ACE中∠AEC=80°,
在Rt△ADE中∠EFD=90°﹣80°=10°.
(2)∠EFD=![]() (∠C﹣∠B)
(∠C﹣∠B)
证明:∵AE平分∠BAC,
∴∠BAE=![]() =90°﹣
=90°﹣![]() (∠C+∠B)
(∠C+∠B)
∵∠AEC为△ABE的外角,
∴∠AEC=∠B+90°﹣![]() (∠C+∠B)=90°+
(∠C+∠B)=90°+![]() (∠B﹣∠C)
(∠B﹣∠C)
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°﹣90°﹣![]() (∠B﹣∠C)
(∠B﹣∠C)
∴∠EFD=![]() (∠C﹣∠B)
(∠C﹣∠B)
(3)∠EFD=![]() (∠C﹣∠B).
(∠C﹣∠B).
如图,
∵AE平分∠BAC,
∴∠BAE=![]() .
.
∵∠DEF为△ABE的外角,
∴∠DEF=∠B+![]() =90°+
=90°+![]() (∠B﹣∠C),
(∠B﹣∠C),
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°﹣90°﹣![]() (∠B﹣∠C)
(∠B﹣∠C)
∴∠EFD=![]() (∠C﹣∠B).
(∠C﹣∠B).
【解析】(1)由三角形内角和定理可得∠BAC=100°,∠CAD=40°,由角平分线的性质易得∠EAC的度数,可得∠EFD;
(2)由角平分线的性质和三角形的内角和得出∠BAE=90°﹣![]() (∠C+∠B),外角的性质得出∠AEC=90°+
(∠C+∠B),外角的性质得出∠AEC=90°+![]() (∠B﹣∠C),在△EFD中,由三角形内角和定理可得∠EFD;
(∠B﹣∠C),在△EFD中,由三角形内角和定理可得∠EFD;
(3)与(2)的方法相同.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列关于x的单项式,探究其规律:x,3x2 , 5x3 , 7x4 , 9x5 , 11x6 , ….按照上述规律,第2016个单项式是( )
A.4031x2015
B.4030x2016
C.4029x2015
D.4031x2016 -
科目: 来源: 题型:
查看答案和解析>>【题目】六边形的内角和是( )
A.540°
B.720°
C.900°
D.1080° -
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值不大于6的整数的积是_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【新知理解】
如图①,若点
 、
、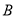 在直线l同侧,在直线l上找一点
在直线l同侧,在直线l上找一点 ,使
,使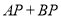 的值最小.
的值最小.作法:作点
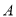 关于直线l的对称点
关于直线l的对称点 ,连接
,连接 交直线l于点
交直线l于点 ,则点
,则点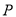 即为所求.
即为所求.【解决问题】
如图②,
 是边长为6cm的等边三角形
是边长为6cm的等边三角形 的中线,点
的中线,点 、
、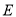 分别在
分别在 、
、 上,则
上,则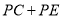 的最小值为 cm;
的最小值为 cm;【拓展研究】
如图③,在四边形
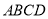 的对角线
的对角线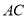 上找一点
上找一点 ,使
,使 .(保留作图痕迹,并对作图方法进行说明)
.(保留作图痕迹,并对作图方法进行说明)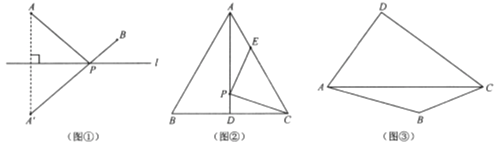
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.
(1)求∠MON的大小;
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?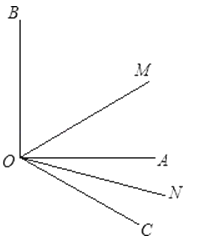
-
科目: 来源: 题型:
查看答案和解析>>【题目】“六一”期间,某商店将单价标为130元的书包按8折出售可获利30%,该书包每个的进价是( )
A. 65元 B. 80元 C. 100元 D. 104元
相关试题

