【题目】如图:已知等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.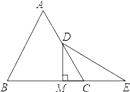
(1)求∠E的度数.
(2)求证:M是BE的中点.
参考答案:
【答案】
(1)解:∵三角形ABC是等边△ABC,
∴∠ACB=∠ABC=60°,
又∵CE=CD,
∴∠E=∠CDE,
又∵∠ACB=∠E+∠CDE,
∴∠E= ![]() ∠ACB=30°;
∠ACB=30°;
(2)证明:连接BD,

∵等边△ABC中,D是AC的中点,
∴∠DBC= ![]() ∠ABC=
∠ABC= ![]() ×60°=30°
×60°=30°
由(1)知∠E=30°
∴∠DBC=∠E=30°
∴DB=DE
又∵DM⊥BC
∴M是BE的中点.
【解析】(1)根据等边三角形的性质得出∠ACB的度数,由CE=CD得出∠E=∠CDE,再根据三角形的一个外角等于和它不相邻的两内角之和,求出∠E的度数。
(2)抓住已知条件等边△ABC中,D是AC的中点,由等腰三角形的三线合一的性质,可知应连接BD,得出BD平分∠ABC,求出∠DBC的度数,继而证得DB=DE,再根据等腰三角形的性质即可证得结论。
【考点精析】关于本题考查的等边三角形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正数m的两个平方根是2a+1和a﹣7,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简(2x-3)2 -(x+y)(x-y)-y2 =________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】气温由-5℃上升了4℃时的气温是( )
A.-1℃B.1℃C.-9℃D.9℃
-
科目: 来源: 题型:
查看答案和解析>>【题目】2020年南充市各级各类学校学生人数约为1 150 000人,将1 150 000 用科学计数法表示为( )
A.1.15×106B.1.15×107C.11.5×105D.0.115×107
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.3a+2b=5abB.3a·2a=6a2C.a3+a4=a7D.(a-b)2=a2-b2
-
科目: 来源: 题型:
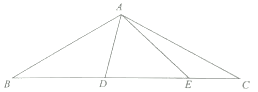
查看答案和解析>>【题目】如图△ABC中,AB=AC,∠BAC=120°,∠DAE=60°,BD=5,CE=8,则DE的长为 .
相关试题

