【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张.

(1)请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果(卡片用A,B,C,D表示);
(2)我们知道,满足![]() 的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.
的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.
参考答案:
【答案】(1)答案见解析;(2)![]() .
.
【解析】
试题分析:(1)利用树状图展示12种等可能的结果数;
(2)根据勾股数可判定只有A卡片上的三个数不是勾股数,则可从12种等可能的结果数中找出抽到的两张卡片上的数都是勾股数的结果数,然后根据概率公式求解.
试题解析:(1)画树状图为:

共有12种等可能的结果数;
(2)抽到的两张卡片上的数都是勾股数的结果数为6,所以抽到的两张卡片上的数都是勾股数的概率=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,下列说法正确的是( )
A.两直线的位置关系是平行、垂直和相交
B.不平行的两条直线一定互相垂直
C.不垂直的两条直线一定互相平行
D.不相交的两条直线一定互相平行 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.
(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°
①求证:AD=BE;
②求∠AEB的度数.
(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=
 CM+
CM+ BN.
BN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的材料:
点A,B在数轴上分别表示有理数a,b,A,B两点之间的距离表示为|AB|.
(1)当A,B两点中有一点在原点时,假设点A在原点,如图①所示,|AB|=|OB|=|b|=|a-b|.


① ②


③ ④
(2)当A,B两点都不在原点时
①如图②所示,点A,B都在原点的右边时,|AB|=|OB|-|OA|=b-a=|a-b|;
②如图③所示,点A,B都在原点的左边时,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|.
③如图④所示,点A,B在原点的两侧时,|AB|=|OA|+|OB|=|a|+|b|=a+(-b)=|a-b|.
解答下列问题:
(1)数轴上表示4与2015的两点之间的距离为________,数轴上表示-
 与-
与-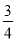 的两点之间的距离为________,数轴上表示1.28与-8.62的两点之间的距离为__________.
的两点之间的距离为________,数轴上表示1.28与-8.62的两点之间的距离为__________.(2)有理数-6和x在数轴上的对应点分别为点A、B,如果|AB|=10,那么x为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆周率π=3.1415926…,将π精确到千分位的结果是( )
A.3.1
B.3.14
C.3.141
D.3.142 -
科目: 来源: 题型:
查看答案和解析>>【题目】某种细菌在培养过程中,每半小时分裂一次(由一个分裂成两个),若这种细菌由1个分裂为64个,则这个过程要经过( )
A. 1小时 B. 2小时 C. 3小时 D. 4小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+2S2+2S3+S4= .

相关试题

