【题目】如图,AF是△ABC的高,AD是△ABC的角平分线,∠B=36°,∠C=76°,求∠DAF的度数. 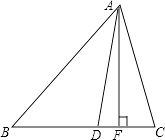
参考答案:
【答案】解:由三角形的外角性质知:∠ADF=∠B+ ![]() ∠BAC, 故∠B+
∠BAC, 故∠B+ ![]() ∠BAC+∠DAF=90°;①
∠BAC+∠DAF=90°;①
△ABC中,由三角形内角和定理得:
∠C+∠B+∠BAC=180°,
即: ![]() ∠C+
∠C+ ![]() ∠B+
∠B+ ![]() ∠BAC=90°,②
∠BAC=90°,②
②﹣①,得:
∠DAF= ![]() (∠C﹣∠B)=20°
(∠C﹣∠B)=20°
【解析】在△ADF中,由三角形的外角性质知:∠ADF=∠B+ ![]() ∠BAC,所以∠B+
∠BAC,所以∠B+ ![]() ∠BAC+∠FAD=90°,联立△ABC中,由三角形内角和定理得到的式子,即可推出∠DAF,∠B,∠C的关系,再代值求解即可.
∠BAC+∠FAD=90°,联立△ABC中,由三角形内角和定理得到的式子,即可推出∠DAF,∠B,∠C的关系,再代值求解即可.
【考点精析】本题主要考查了角的平分线和三角形的内角和外角的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.

(1)若BE⊥AC,CD⊥AB,求∠BHC的度数.
(2)若BE、CD平分∠ABC和∠ACB,求∠BHC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某人走进一家商店,进门付l角钱,然后在店里购物花掉当时他手中钱的一半,走出商店付1角钱;之后,他走进第二家商店付1角钱,在店里花掉当时他手中钱的一半, 走出商店付1角钱;他又进第三家商店付l角钱,在店里花掉当时他手中钱的一半,出店付1角钱;最后他走进第四家商店付l角钱,在店里花掉当时他手中钱的一半, 出店付1角钱,这时他一分钱也没有了.该人原有钱的数目是角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如表所示:
A
B
进价(万元/套)
1.5
1.2
售价(万元/套)
1.65
1.4
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少的数量的1.5倍.若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x3+x2=x5B.(x﹣3)2=x2﹣9
C.(x2)3=x5D.5x2x3=5x5
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:a2+2ab= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x、y均为正整数,且2x2y=128,则x+y的值为( )
A. 5 B. 6 C. 7 D. 8
相关试题

