【题目】已知函数y=ax2+bx+c(a≠0)的图象与函数y=x﹣ ![]() 的图象如图所示,则下列结论:①ab>0;②c>﹣
的图象如图所示,则下列结论:①ab>0;②c>﹣ ![]() ;③a+b+c<﹣
;③a+b+c<﹣ ![]() ;④方程ax2+(b﹣1)x+c+
;④方程ax2+(b﹣1)x+c+ ![]() =0有两个不相等的实数根.其中正确的有( )
=0有两个不相等的实数根.其中正确的有( ) 
A.4 个
B.3 个
C.2 个
D.1 个
参考答案:
【答案】B
【解析】解:∵抛物线开口朝上, ∴a>0,
∵对称轴x=﹣ ![]() 在y轴的右侧,
在y轴的右侧,
∴b<0,
∴ab<0,故①错误;
∵抛物线与y轴的交点在直线的上方,
∴c>﹣ ![]() ,故②正确;
,故②正确;
当x=1时,ax2+bx+c<x﹣ ![]() ,即a+b+c<﹣
,即a+b+c<﹣ ![]() ;故③正确;
;故③正确;
∵函数y=ax2+bx+c(a≠0)的图象与函数y=x﹣ ![]() 的图象有两个不同的交点,
的图象有两个不同的交点,
∴ax2+(b﹣1)x+c+ ![]() =0有两个不相等的实数根,故④正确.
=0有两个不相等的实数根,故④正确.
故选B.
【考点精析】利用求根公式和二次函数图象以及系数a、b、c的关系对题目进行判断即可得到答案,需要熟知根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).
-
科目: 来源: 题型:
查看答案和解析>>【题目】据报道,深圳今年4 月2 日至4 月8 日每天的最高气温变化如图所示.则关于这七天的最高气温的数据,下列判断中错误的是( )
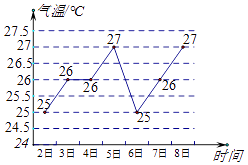
A.平均数是26
B.众数是26
C.中位数是27
D.方差是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在菱形ABCD中,∠A=60°,AB=2,E,F两点分别从A,B两点同时出发,以相同的速度分别向终点B,C移动,连接EF,在移动的过程中,EF的最小值为( )

A. 1 B.
 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知五边形ABCDE 是⊙O 的内接正五边形,且⊙O 的半径为1.则图中阴影部分的面积是( )
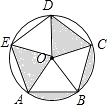
A.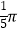
B.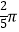
C.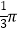
D.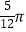
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=2,BC=4,P为矩形边上的一个动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以A,P,B为顶点的三角形面积为y,则选项图象能大致反映y与x的函数关系的是( )
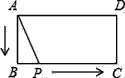
A.
 B.
B. 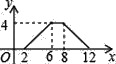 C.
C. 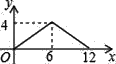 D.
D. 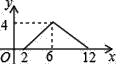
-
科目: 来源: 题型:
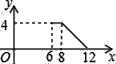
查看答案和解析>>【题目】如图,甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.分析甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分钟)变化的函数图象,解决下列问题:
(1)求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式;
(2)甲行驶10分钟后,甲、乙两人相距多少千米?

-
科目: 来源: 题型:
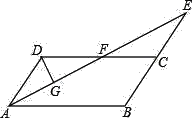
查看答案和解析>>【题目】如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
(1)求证:CD=BE;
(2)若AB=4,点F为DC的中点,DG⊥AE,垂足为G,且DG=1,求AE的长.
相关试题

